生物科学研究所井口研究室

Laboratory of Biology, Okaya, Nagano, Japan

Home

回帰と相関，知っているようで知らない，その本質：Excel の回帰分析を例として

井口豊（生物科学研究所，長野県岡谷市）
最終更新：2024 年 8 月 8 日

1. はじめに

このページでは，回帰直線とはどのようなものなのか理論的に考え，最小二乗法による直線回帰の「誤解」について取り上げたい。特に， Microsoft の Excel （エクセル）を用いて回帰分析の具体例を示し，その理論的背景を考えてみたい。

これは，読んで字のごとく，データ点からの二乗和が最小になる近似式（適合式），を求めるものである。ところが，この「データ点からの距離」の取り方が，「くせもの」なのである。

最小二乗法は頻繁に行われる直線近似法である。 Excel などの表計算ソフトでも容易に出来る。しかし，それがゆえに，どんな計算法か知らずに適用されてきているのも事実である。

ここでは，最も単純な 2 変数 x, ｙのデータを使った最小二乗法による直線（いわゆる回帰直線， regression line）への適合と検定について考える。ここでの計算は，一般的に最小二乗法（Least squares method）と呼ばれている，通常最小二乗法（Ordinary Least Square: OLS）である。わざわざ「通常」と呼ばれるからには，通常でない最小二乗法もあることを念頭において欲しい。以下，この通常最小二乗法を単に，最小二乗法と呼ぶ。

一方で，二乗でなく絶対値の和が最小となる回帰式も当然ある。それを最小絶対値法（Least absolute value method）による回帰と呼ぶ。これが意外と知られておらず，回帰や近似と言えば，最小二乗が当然だと思い込んでいる人も多い。それに関しては，次のページの解説参照：（最小二乗と最小絶対値：ロバスト回帰で外れ値分析）。

その他の回帰について，土浦協同病院の倉持龍彦さんが中心となり，私を含む統計解析研究グループの成果が次の論文である。

倉持龍彦・井口豊 (2020)
“R言語”が導く統計解析の世界
血液浄化とそれを支える基盤技術，織田成人・酒井清孝（編），東京医学社：167-182.

倉持龍彦・對馬栄輝・下井俊典・井口豊・宮田賢宏・大塚紹・大友学・若狭伸尚・村野勇・米津太志・角田恒和（2018）
統計解析を用いた信頼性の評価 2
医工学治療 30 (3): 149-155.

そこでは，通常回帰，主成分回帰， Deming 回帰，幾何平均回帰，Passing-Bablock 回帰を解説している。簡単に図示すると，以下のような計算である（同論文の図 5 を簡略化）。

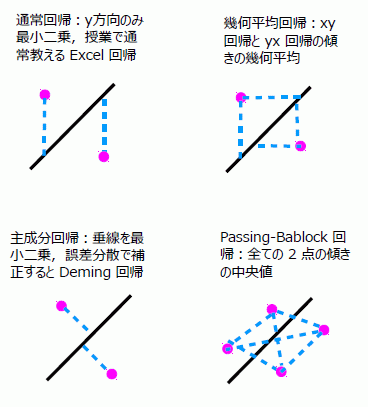
通常回帰，主成分回帰， Deming 回帰，幾何平均回帰，Passing-Bablock 回帰グラフ

主成分回帰は，主軸回帰，最大軸回帰などとも呼ばれ， MA (Major axis）回帰と略されることも多い。幾何平均回帰は，標準化主軸回帰（Standardised major axis）と呼ばれ， SMA 回帰と略されることも多いが，標準主軸 (Standard major axis）回帰，縮小長軸（Reduced major axis, RMA）回帰と呼ばれることもある。両回帰とも用語に混乱がある。これらの回帰の特徴に関しては，以下のページを参照してほしい。

回帰分析: x, y 誤差がある場合 SMA, MA 回帰

再度述べるが，これらの回帰のうち，以下に解説するのは通常回帰である。

「回帰」と「相関」の統計学的な研究のパイオニアとなったのは， Francis Galton （進化論で有名な Charles Darwin の従兄弟）と Karl Pearson である。これに関しては，別ページに参考文献やサイトを挙げた。

標準偏差の名付け親は，相関係数で有名なピアソン，不偏標準偏差の話題と共に

相関係数を表す r は， Galton が唱えた「先祖返り（reversion）」に由来するとされ，この reversion が，その後の regression （回帰）に相当する。次の文献参照。

Rao, C. R. (1983)
多変量解析その起源と発展に関する回想
応用統計学 12(2): 69-78 (柳井晴夫・竹内啓訳）.

Excel における R2 (決定係数) や補正 R2 (自由度調整済み決定係数) の問題点は，以下のページを参照してほしい。

2. 回帰直線は，どのようにして決まるか？

次のような 8 個の対から成るデータ， x, y を考えよう。

    -------------
       x     y
    -------------
       0      45
       5      25
       6      75
      11      55
      12     105
      17      85
      18     135
      23     115
    --------------

Excel のグラフ作成機能で作った散布図（ Scatter Diagram）が図 1。この散布図の場合は，本当は 2 つの右上がりの直線に適合させるべきであるが，回帰分析の学習だと思って，単一直線への適合を考えてみよう。

左は，例えば小中学生などがやる，最も適合しそうだと直感で（勘で），記入される直線。大人でも，こんな直線を引くのではないかと思うし，私も理解できる。

一方，右は，グラフのデータ点を右クリックして，

グラフの近似曲線の追加　→　オプション　→　線形近似→　オプション→　「グラフに数式を表示する」と「R2乗値を表示する」

を選んで示された直線と線形（つまり，一次関数の）回帰式である。これは，最小二乗法で作成された直線でもある。

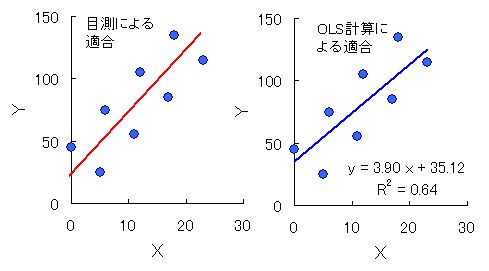
目測による直線適合（左）と最小二乗法による直線適合（右）

図１. 同一データについて，目測による直線適合（左）と最小二乗法による直線適合（右）．

回帰式を求めるだけなら，もとの表で

挿入　→　関数

とたどって， SLOPE 関数と INTERCEPT 関数からも求められる。

左右のグラフの直線の傾きに注目して欲しい。右の最小二乗法では， x が大きくなるほど，直線が下側へズレている。

なぜ，このようになるのだろうか？

これは図 2 に示すように，最小二乗法が縦方向，つまりｙ軸方向の距離のみを最小とするように計算されているからである。だから，単純に点と点の中間を通るような直線にはならないのである。

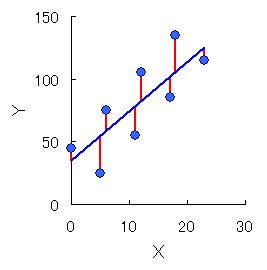
最小二乗法によるデータ点から直線までの距離の計算でｙ軸方向のみ最小化される

図 2. 最小二乗法によるデータ点から直線までの距離の計算でｙ軸方向のみ最小化される．

一般的には，変数 x は独立変数または説明変数と呼ばれ，変数 y は従属変数または目的変数と呼ばれる。図 2 から分かるように，変数 x は誤差を含まないと仮定されるため，確定変数または固定変数（fixed variable）と呼ばれることもある。

3. 最小二乗法の理論的計算

では，最小二乗法とは，どのような計算で，回帰直線は，どのように決定されるのだろうか？

まず，回帰式として次のような１次関数を想定する。

\begin{equation} y = a x + b \tag{1a} \end{equation}

ここで a, b はパラメータと呼ばれる定数である。当然だが，２次関数とか，その他の非線形関数とかを想定する場合もありうる。

ある点 x_i における観測値を y_i として，その時の計算値 Y_i との差 E を考える。

\begin{equation} E = y_i + Y_i \end{equation}

これを残差（residual）と呼ぶ。最小二乗法とは，全ての点について，この残差の 2 乗を求め，その総和 Q 最小になるように，パラメータ a, b を決定する方法である。

\begin{align} Q &= \sum E^2 \\ &= \sum (y_i - Y_i)^2 \\ &= \sum \{y_i - (a x_i + b)\}^2 \tag{1b} \end{align}

なお，a は直線の傾きを表すが，回帰では回帰係数と呼ぶ。

この式からも分かるように，y 軸方向の距離だけを最小にする，これが最小二乗法の本質だと言える。

ここで，「本質」と述べたのは，ここで取り上げた 1 次関数に限らず， 2 次関数だろうが，その他の非線形関数だろうが，同様の方法でパラメータを決定するからである。

式 (1b) の x_i， y_i には測定値が入るので，結局，この式は変数 a, b の式と見ることができる。したがって， Q の最小値を求めるためには， a, b で偏微分して，その連立方程式を解けば良い。

式を見やすくするために，あらためて次のようにおく。

\begin{align} x &= x_i \\ y &= y_i \end{align}

その上で，Q を a, b で偏微分して

\begin{align} \frac{\partial Q}{\partial a} &= -2\sum x \{y - (ax + b) \} \\ \frac{\partial Q}{\partial b} &= -2\sum \{y - (ax + b) \} \end{align}

それぞれ = 0 と置いて

\begin{align} & \sum xy - a\sum x^2 - b\sum x = 0 \tag{2a} \\ & \sum y - a\sum x - b n = 0 \tag{2b} \end{align}

これを，まず a について解くと，以下のようになる。

\begin{equation} a=\frac{\sum xy - \frac{\sum x \sum y}{n}}{\sum x^2 - \frac{(\sum x)^2}{n}} \tag{3} \end{equation}

これを整理すると，以下のようになる。

\begin{equation} a=\frac{\sum (x-m_x)(y-m_y)}{\sum (x-m_x)^2} \tag{4} \end{equation}

ここで，m_x, m_y は，それぞれ x, y の平均を表す。 (3)，(4) のどちらを使っても良いが，(4) の方が，傾き a の性質を直感的に理解しやすい。

一方， b については，式 (2b) より，

\begin{align} b &= \frac{\sum y}{n} - a \frac{\sum x}{n} \\ &= m_y - a \; m_x \tag{5} \end{align}

元の式（1a）に，この式 (5) を代入すると

\begin{align} y &= ax + b \\ &= ax + m_y - a \; m_x \\ &= a(x - m_x) + m_y \tag{6} \end{align}

すなわち，回帰直線は， x, y の平均の点　\( (m_x, m_y) \) を必ず通過する。この点をデータの重心と呼ぶ。

回帰直線がデータの重心を通るという性質は，この後，データの変動や統計量の検定を考えるとき重要となる要素である。

4. 回帰係数，相関係数，決定係数の違い

では，回帰係数（= 傾き）と相関係数は，どのように違うのだろうか？

式 (3) と式 (4) の傾き a の分母の計算に注意して欲しい。x のみで決まり，y は全く関係しないのである。これは x の平均からの変化に伴って， y がその平均からどう変化するかを表した式といっても良い。

「そんなこと \(y = ax + b \) の式なんだから，言われなくても分かる」と言うかもしれないが，これが意外と理解されてないのである。

例えば， x, y を入れ替えたデータから出来る回帰直線は，改めて y 軸方向の残差が最小になるようにして得られる直線であり，元の直線の x, y を入れ替えて出来る直線と必ずしも一致しないのである。

あとで具体例を示すが， x, y を入れ替えたデータから出来る回帰直線は，必ずしも元の直線の逆関数とはならないのである。

一方，通常，相関係数と呼ばれる，積率相関（Pearson 相関）係数 r は次のように計算される。

\begin{equation} r=\frac{\sum (x-m_x)(y-m_y)}{\sqrt{\sum (x-m_x)^2 \sum (y-m_y)^2}} \tag{7} \end{equation}

これは， x, y に関して対称式であり， x, y を入れ替えても全く同じ式となる。これが， Excel の CORREL 関数の計算式である。

つまり，回帰係数は， y に対する x の関係，という一方通行的な係数なのに対し，相関係数は，x と y 相互間の関係，という双方向な係数なのである。統計データの分析に携わる人の中にも，この点を十分理解せずに，回帰と相関を利用している人がいるので注意してほしい。

さらに，単回帰式における標準回帰係数は，相関係数（Pearson 相関係数）に等しくなる，ということも，知っておくべきである。

標準回帰係数と相関係数

ここで，相関係数の分母（偏差平方和）と分子（積和）の大小関係を見てみよう。

n 個の x，y データについて，その各偏差をベクトル x，y の成分として考える。

\begin{align} \boldsymbol{x} &= (x_1 - m_x, x_2 - m_x, ... x_n-m_x) \\ \boldsymbol{y} &= (y_1 - m_y, y_2 - m_y, ... y_n-m_y) \end{align}

すると，積和 \( \sum (x - m_x)(y - m_y) \) は，ベクトル x，y の内積と考えられる。

\begin{align} [\boldsymbol{x}, \boldsymbol{y}] = &(x_1 - m_x)(y_1 - m_y) \\ &+ (x_2- m_x)(y_2 - m_y) \\ &+ ... + (x_n - m_x)(y_n - m_y) \end{align}

同様に， x の偏差平方和 \( \sum (x - m_x)^2 \) と y の偏差平方和 \( \sum (y - m_y)^2 \) は，それぞれベクトル x，y の大きさ（絶対値）の 2 乗と考えられる。

\begin{align} |\boldsymbol{x}| = &(x_1 - m_x)^2 + (x_2- m_x)^2 +(x_n - m_x)^2 \end{align}

\begin{align} |\boldsymbol{y}| = &(y_1 - m_y)^2 + (y_2- m_y)^2 +(y_n - m_y)^2 \end{align}

ここで，コーシー・シュワルツ（Cauchy–Schwarz）の不等式より，

\begin{align} |(x, y)| \leq |x||y| \end{align}

よって，積和と偏差平方和の関係は以下のようになる。

\begin{align} |\sum(x - m_x)(y - m_y)| \leq \sqrt{\sum (x - m_x)^2} \sqrt{\sum (y - m_y)^2} \end{align}

すなわち

\begin{align} \frac{|\sum(x - m_x)(y - m_y)|}{\sqrt{\sum (x - m_x)^2} \sqrt{\sum (y - m_y)^2}} \leq 1 \end{align}

となり，相関係数の絶対値が 1 以下であることが証明される。

コーシー・シュワルツの不等式を利用すると，相関係数の分子の絶対値の大きさが，分母の大きさによって抑えられていることが良く分かる。

式 (4) で，回帰の傾き a を，もう一度見て欲しい。分母の式から，y に対する x の関係，という一方通行的な統計量であることは既に述べた。

しかし，この分母を以下のように分解して

\begin{align} \sum (x-m_x)^2 = \sqrt{\sum (x-m_x)^2} \sqrt{\sum (x-m_x)^2} \end{align}

と分解し，ひとつのルート内の x を y に入れ替えたのが，相関係数 r なのである。

つまり，相関係数の分母では，x の偏差平方和と y の偏差平方和の相乗平均を取り，x の変化も y の変化も考慮しているのである。

ちなみに，x と y の積の平方根

\begin{align} \sqrt{xy} \end{align}

これを相乗平均と言い，相加平均との関係で高校時代に学んだ人も多いだろう。

ところで，x, y 相互間の結びつきの強さを示すには，相関係数ｒより，それを 2 乗したｒ² を用いるほうが良い。

\begin{align} r^2 = \frac{\{\sum(x - m_x)(y - m_y)\}^2}{\sum (x - m_x)^2 \sum (y - m_y)^2} \end{align}

これを決定係数（coefficient of determination）と呼ぶ。

ただし，注意してほしいのは，これは複数ある決定係数の定義の一つに過ぎないということである。これに関しては，以下のページの解説参照してほしい。

この決定係数は，回帰係数と結びつきが強く，その意味でも統計学上の重要な指標である。

例えば，決定係数を以下のように，変形してみる。

\begin{equation} r^2=\frac{\sum (x-m_x)(y-m_y)}{\sum (x-m_x)^2}\frac{\sum (x-m_x)(y-m_y)}{\sum (y-m_y)^2} \tag{8} \end{equation}

ここで，右辺の左の分数は回帰による y 方向の変動を表すことは以下のように証明できる。

まず，第 3 章冒頭に述べたように，測定値 x を回帰直線に代入して得られる値を Y とする。

すなわち，

\begin{equation} Y = a x + b \tag{9} \end{equation}

y の計算値（推定値） Y と y の測定値の平均 m_y との差の平方和 Sr は以下のとおり。

\begin{equation} Sr = \sum (Y - m_y)^2 \tag{10} \end{equation}

これが，回帰による（回帰直線上の） y 方向の変動量である。

ここで，求める回帰直線が重心 \( (m_x, m_y) \) を通ることに注目する。

\begin{equation} m_y = a \: m_x + b \tag{11} \end{equation}

さらに，式 (9) (11) を (10) に代入し整理する。

\begin{align} Sr &= \sum \{ax + b - (a \: m_x + b) \}^2 \\ &= \sum a^2(x - m_x)^2 \\ &= a^2 \sum(x - m_x)^2 \tag{12} \end{align}

ここで，式 (4) の傾き a を再度取り上げる。

\begin{align} a=\frac{\sum (x-m_x)(y-m_y)}{\sum (x-m_x)^2} \tag{4} \end{align}

この a を式 (12) に代入すると以下のようになる。

\begin{align} Sr &= \left\{\frac{\sum (x-m_x)(y-m_y)}{\sum (x-m_x)^2}\right\}^2 \sum (x - m_x)^2 \\ &= \frac{\left\{\sum (x-m_x)(y-m_y)\right\}^2}{\sum (x-m_x)^2} \end{align}

さらにこの Sr を決定係数の式 (8) に代入すると以下のようになる。

\begin{align} r^2 &= \frac{\left\{\sum (x-m_x)(y-m_y)\right\}^2}{\sum (x-m_x)^2} \frac{1}{\sum (y - m_y)^2} \\ &= Sr \frac{1}{\sum (y - m_y)^2} \end{align}

ここで，最後の式の分母は， データの y 方向の全変動を表すので，これを以下のようにおく。

\begin{equation} Sy = \sum (y - m_y)^2 \tag{13} \end{equation}

結局，次のように表せる。

\begin{align} r^2 = \frac{Sr}{Sy} \tag{14} \end{align}

すなわち，決定係数 r² は，y 軸方向の全変動量 Sy に占める回帰変動量 Sr の割合を表す指標とも言えるのである。

相関係数が，x, y 相互間の双方向な関係を表す統計量である，と既に述べた。一方，決定係数は，相関係数を 2 乗しただけであるが，随分異なる性質を持つことが理解できるだろう。

ところで，相関係数が 0，つまり無相関なら，回帰係数（= 傾き）はどうなるだろうか？傾き a の式 (4) と相関係数の式 (7) を再び見よう。

\begin{equation} a=\frac{\sum (x-m_x)(y-m_y)}{\sum (x-m_x)^2} \tag{4} \end{equation}

\begin{equation} r=\frac{\sum (x-m_x)(y-m_y)}{\sqrt{\sum (x-m_x)^2 \sum (y-m_y)^2}} \tag{7} \end{equation}

相関係数が 0 の時を考えると， r において分母が 0 にならず，分子が 0 となる時である。その時，回帰係数 a の分母も 0 にならず，分子は 0 となる。すなわち，相関係数が 0 ならば，回帰係数（= 傾き）も 0 なのである。このことを理解していない人がかなり多い。

さらに厳密に，相関係数 0 （無相関）の検定と，回帰直線の傾き（回帰係数）0 の検定が，同等のものであることは，このページ末の注 3 に示した。

なお，相関係数の強弱の基準には，ギルフォードの基準（Guilford's Rule of Thumb）が広く用いられる。それに関しては，以下のページの解説を参照してほしい。

統計学の基準値の由来：5%有意水準，カイ二乗検定，相関係数の出典と引用

日本語の統計学の教科書やウェブサイトでは，相関係数の強弱の区分が示されることは多いが，Guilford の名前や文献が挙がることは稀である。相関係数の強弱区分は慣用的である，ということで済ませている場合も多い。

5. 最小二乗法のデータへの適用

ここでは，第 2 章冒頭に示した 8 対の x, y のデータに最小二乗法を適用し，回帰直線を求めてみよう。

まず， x, y の平均をそれぞれ求める。

\begin{align} m_x &= 11.5 \\ m_y &= 80 \end{align}

これら平均と，各 x, y の差（偏差）を求める。 Excel では，表 1 のような計算を，まず行う。

表1. 最小二乗法で回帰直線を求めるときの基本計算

回帰直線を求めるときの基本計算

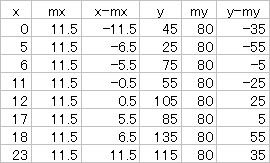
ここから， x と y の偏差積和，および，x の偏差平方和を以下のように計算する。

\begin{align} &\sum (x - m_x)(y - m_y) = 1600 \\ &\sum (x - m_x) ^2 = 410 \end{align}

したがって，式　(4)　より，直線の傾き a は，

\begin{align} a &= \frac{1600}{4} \\ &= 3.9024 \end{align}

また，式 (6) より，回帰直線は，重心を通るので，

\begin{align} m_y = a\: m_x + b \end{align}

よって，

\begin{align} b &= m_y - a\: m_x \\ &= 80 - 3.9024*11.5 \\ &= 35.122 \end{align}

結局，回帰直線は次のようになる。

\begin{equation} y = 3.9024x + 35.122 \tag{15} \end{equation}

これが図 1 右に示した EXCEL グラフの回帰直線の式である。

ここで，最小二乗法の定義式として，式 (1b) をもう一度取り上げよう。

\begin{align} Q = \sum \{y_i - (a x_i + b)\}^2 \tag{1b} \end{align}

少し面倒だが，実際に，この式に測定値（表1の x と y）を入れて計算してみよう。

\begin{align} Q = &\{45 - (a*0 + b)\}^2 \\ &+ \{25 - (a*5 + b)\}^2 \\ &+ \{75 - (a*6 + b)\}^2 \\ &+ \{55 - (a*11 + b)\}^2 \\ 　 &+ \{105 - (a*12 + b)\}^2 \\ &+ \{85 - (a*17 + b)\}^2 \\ &+ \{135 - (a*18 + b)\}^2 \\ &+ \{115 - (a*23 + b)\}^2 \\ \end{align}

展開，整理すると

\begin{align} Q = &1468a^2 - 17920a \\ &+ 8b^2 - 1280b \\ &+ 184ab + 61000 \end{align}

したがって， Q は， a, b の 2 次曲面となる。

グラフ描画ソフト gnuplot を使って，この関数の 3 次元プロットを見よう（図 3）。「すりばち」を横から押しつぶしたような形状であり，最小値が (a, b) = (4, 40) 付近だと視覚的に確認できる。

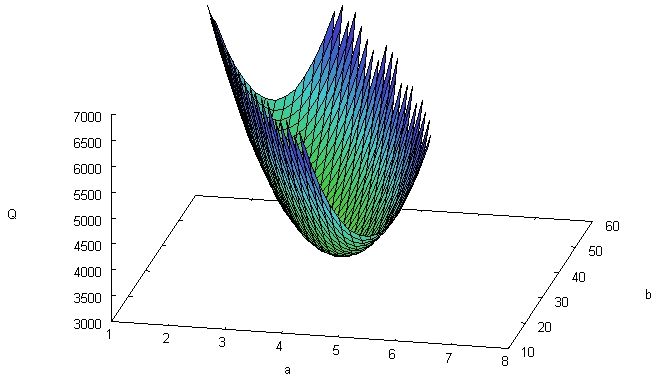
最小二乗曲面 Q

図3. 最小二乗曲面 Q

図 4 のように，Q-a 面の方向，つまり， a 軸を真横から見ると，a の最小値が 4 付近にあることが理解できる。

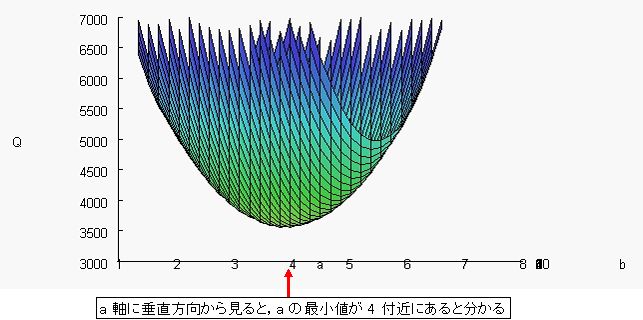
最小二乗曲面 Q の Q-a 面

図4. 最小二乗曲面 Q の Q-a 面

さらに，図 5 のように，Q-b 面の方向，つまり，b 軸を真横から見ると，b の最小値が 30 から 40 付近にあると良く分かる。

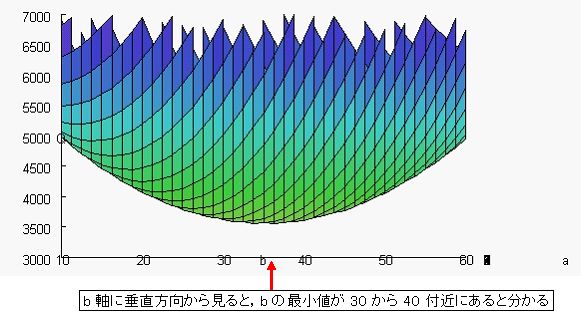
最小二乗曲面 Q の Q-b 面

図 5. 最小二乗曲面 Q の Q-b 面

これらが， a, b の最小値，3.9024 と 35.122 を幾何学的に表現している。

ここで，先ほど述べた x, y を入れ替えたデータから出来る回帰直線は，改めて y 軸方向の残差が最小になるようにして得られる直線であり，元の直線の x, y を入れ替えて出来る直線と必ずしも一致しない，ということを思い出して欲しい。

例えば，今まで見てきた回帰直線

\begin{align} y = 3.9024x + 35.122 \tag{15} \end{align}

この x と y を入れ替えて，逆関数を考えよう。

\begin{align} x = 3.9024y + 35.122 \end{align}

として，y について整理すると，

\begin{align} y = 0.25625x - 9.000 \end{align}

一方，データの x と y を入れ替えて，回帰直線を求めると以下のようになる。

\begin{align} y = 0.16327x - 1.5612 \end{align}

これは逆関数とは全く異なる式となる。統計を頻繁に扱う人でも，この点を認識不足の人がいる。十分注意してもらいたい点である。

ところで，前章の最後に触れた，相関係数が 0 の時の具体例を見るため，次のような（x, y）のデータを考えよう。

\begin{align} \boldsymbol{x}= \begin{bmatrix} 1 \\ \frac{1}{\sqrt{2}} \\ 0 \\ -\frac{1}{\sqrt{2}} \\ -1 \\ -\frac{1}{\sqrt{2}} \\ 0 \\ \frac{1}{\sqrt{2}} \end{bmatrix}, \: \boldsymbol{y}= \begin{bmatrix} 0 \\ \frac{1}{\sqrt{2}} \\ 1 \\ \frac{1}{\sqrt{2}} \\ 0 \\ -\frac{1}{\sqrt{2}} \\ -1 \\ -\frac{1}{\sqrt{2}} \end{bmatrix} \end{align}

これは，単位円 \(x^2 + y^2 = 1 \) 上に，x 軸上から 45゜ごとに取った点である。その散布図と回帰直線を示す（図 6）。

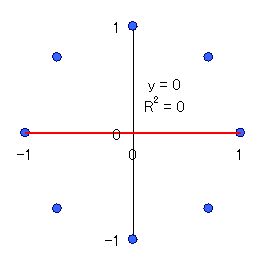
最小二乗曲面 Q の Q-a 面

図 6. 単位円 \(x^2 + y^2 = 1 \) 上に 45゜ごとに取った点の分布と回帰直線（赤）．

相関係数が 0，すなわち無相関であることは，すぐ分かるだろう。しかし，回帰直線が y = 0 であることが，すぐ分かるだろうか？

直感的には，このような分布だと，回帰直線は，どのようにでも引けるとも言えるし，どのようにも引けないとも言えそうだ。

しかし，回帰直線を求める上で重要な2点を，もう一度考えて欲しい。

データ分布の重心を通り，この場合， (0, 0)。
y 方向の最小二乗のみを考える。

そうすると，y = 0 の回帰直線が見えてくるであろう。この場合の最小二乗法定義式の 3 次元プロットも下に示す。

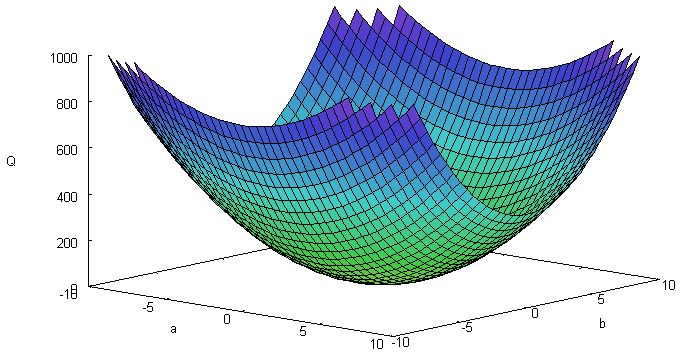
単位円の最小二乗法定義式の3 次元プロット

図7. 単位円 \(x^2 + y^2 = 1 \) 上に 45゜ごとに取ったデータ（図 6）の最小二乗法定義式の 3 次元プロット．

これは \((a, b) = (0, 0) \) で最小値を取る 2 次曲面となる。

6. 回帰の検定

6.1. 係数と定数項がゼロであるかどうかの検定

回帰直線 \(y = ax + b \) のパラメータの検定について考える。厳密な証明は専門書に譲り，ここでは，回帰直線の性質をもとに，標本の平均値についての t 検定からの類推で，パラメータの検定に至る。

なお，回帰式における係数や定数項の検定と言えば，通常は，それらがゼロであるという帰無仮説（null hypothesis）に対する検定である。それらがゼロ以外の場合に対する検定は，6.2. 係数と定数項がゼロ以外の場合に対する検定を参照してほしい。

まず，傾き a の検定を考える。回帰直線は y 軸方向の残差のみが問題となることに再び注意しよう。

すると，測定値 y と計算値 Y の差の平方和（残差平方和）

\begin{align} S_e = \sum (y - Y)^2 \tag{16} \end{align}

これを自由度 n - 2 で割った残差分散（residual variance） Ve を考え，それを回帰直線の誤差分散の不偏推定量（不偏誤差分散）と考えるのは不自然ではない。

この残差分散（不偏誤差分散） Ve を，よく知られた標本不偏分散 s² と対応させると分かりやすいだろう。

\begin{align} s^2 &= \frac{\sum (x - m_x)^2}{n - 1} \\ V_e &= \frac{\sum (y - Y)^2}{n - 2} \tag{17} \end{align}

Ve で，自由度 n - 2 としたのは，標本サイズ n からパラメータ a, b の 2 個分引いたものである。

右式では，平均の周りに正規分布に従って観測値が散らばることを利用し，左式では，回帰直線の周りに正規分布に従って観測値が散らばることを利用している。当然ながら，両者ともデータのバラツキの正規性を前提としているのである。

したがって，この残差分散は回帰直線からのデータのバラツキを表す統計量と言える。誤解されがちだが，決定係数 R² は，そういう意味の指標ではない。それに関しては，別ページの解説参照：決定係数R2は回帰のバラツキ指標ではない。

傾き a の式 (4) をもう一度見よう。

\begin{equation} a=\frac{\sum (x-m_x)(y-m_y)}{\sum (x-m_x)^2} \tag{4} \end{equation}

回帰直線は y 軸方向の残差のみが問題となる，に注目すると， a の標準誤差を考える上で，問題となるのは分子だけである。それゆえ，この式の分子を残差分散 Veで置き換え，その平方根を取ったものを，傾きの標準誤差 Sa と見なすのも不自然ではない。

この傾きの標準誤差 Sa を，よく知られた 平均値の標準誤差 SE と対応させると分かりやすいだろう。

\begin{align} SE &= \sqrt{\frac{s^2}{n}} \\ Sa &= \sqrt{\frac{Ve}{\sum (x-m_x)^2}} \tag{18} \end{align}

平均値では，標本サイズ n を大きくするほど SE が小さくなり，平均値がより正確になる，と理解できる。

一方，傾きでは，x の平均 m_x から離れたデータが増えるほど， Sa は小さくなる。これは，式 (6) に示したように，回帰直線が重心 \((m_x, m_y)\) を通ることから，単に全体の標本サイズを大きくすることより，重心から離れたデータ量を増やした方が，より正確な傾きが得られることは明らかであろう。

この Sa を用いて，回帰直線 (15) について

\begin{equation} y = 3.9024x + 35.122 \tag{15} \end{equation}

その傾き 3.9024 の検定を進める。

まず，元のデータの x 値を，この回帰直線に代入し，元のデータの y 値と計算値 Y の差（残差）を計算する。

表2. 回帰直線からの残差の計算
Y = 3.9024x + 35.122 として計算

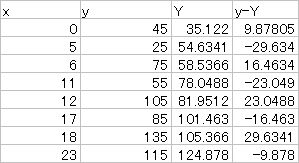
回帰直線からの残差

残差平方和を自由度 n - 2 で割った残差分散 Veを求める。

\begin{align} V_e &= \frac{\sum (y - Y)^2}{n - 2} \\ &= 592.6829 \tag{19} \end{align}

さらに， x の偏差平方和を計算。

\begin{align} \sum (x - m_x)^2 = 410 \tag{20} \end{align}

式 (19) と (20) を (18) に代入して

\begin{align} Sa = \sqrt{\frac{592.6829}{410}} \end{align}

結局，
Sa = 1.2023

求めた回帰直線（15）の傾き 3.9024 が，ある傾き a と異なるかどうかは，t 検定で調べられる。

\begin{align} t = \frac{|3.9024 - a|}{Sa} \tag{21} \end{align}

自由度は
n - 2 = 6

この式 (21) を用いて，傾き 0 に対する検定を行うと，

\begin{align} t &= \frac{|3.9024 - 0|}{1.2023} \\ &= 3.246 \end{align}

自由度 6 に対して，
p = 0.018
という結果が出る。

次に，回帰直線 \( y = ax + b \) の y 切片 b の検定を考えよう。式 (6) に示したように，回帰直線が重心 \( (m_x, m_y) \) を通ることから，

\begin{align} m_y = a \: m_x + b \\ \end{align}

すなわち以下のように置ける。

\begin{align} b = m_y - a \: m_x \\ \end{align}

したがって，b の分散 \(V[b]\) は，

\begin{align} V[b] &= V[m_y - a \: m_x] \\ 　　　&= V[m_y] + V[a \: m_x] + Cov[m_y, b] \end{align}

ここで，回帰直線が傾きいかんに関わらず重心を通る，ということは，\(m_y \) と b が独立であることを示し，

\begin{align} Cov[m_y, b] = 0 \end{align}

また，分散の基本的計算から

\begin{align} V[a \: m_x] = m_x^2 V[a] \end{align}

したがって，

\begin{align} V[b] = V[m_y] + m_x^2 V[a] \end{align}

ここで，\(V[m_y] \) は， y の平均値の分散である。

式 (17) で定義された残差分散（不偏誤差分散） Ve を用い，式 (17) の標本平均の標準誤差 SE からの類推で，

\begin{align} V[m_y] = \frac{V_e}{n} \end{align}

と置ける。

また，\(V[a]\) は傾きの分散だから，式 (18) の傾きの標準誤差 Sa の 2 乗である。

結局，

\begin{align} V[b] &= \frac{V_e}{n} + m_x^2 \frac{V_e}{\sum (x - m_x)^2} \\ &= V_e \left(\frac{1}{n} + \frac{m_x^2}{\sum (x - m_x)^2}\right) \end{align}

したがって， y 切片 b の標準誤差 Sb は，

\begin{align} Sb &= \sqrt{V[b]} \\ &= \sqrt{V_e \left(\frac{1}{n} + \frac{m_x^2}{\sum (x - m_x)^2}\right)} \end{align}

ここで，
標本サイズ: n = 8
x 平均: \( m_x = 11.5 \)

式(18)より，
残差分散: Ve = 592.683

式(19)より，
x 偏差平方和: \( \sum (x - m_x)^2 \) = 410

これらを代入して
Sb =16.2869

求めた回帰直線式 (７）の y 切片 35.122 が 0 と異なるかどうか，すなわち，回帰直線が原点を通るかどうか，やはり t 検定で調べられる。

\begin{align} t &= \frac{|35.122 - 0|}{16.2869} \\ &= 2.157 \end{align}

結局，
ｔ = 2.157
p = 0.074

以上の結果を整理する。

切片 = 35.122, Sb =16.2869, ｔ = 2.157, p = 0.074

傾き = 3.9024, Sa = 1.2023, ｔ = 3.246, p = 0.018

一方，Excelを用いて，

ツール　→　分析ツール　→　回帰分析

とたどって，与えられたデータ \( (x, y) \) を分析した結果は以下の通りである。

表 3. EXCEL 分析ツールの回帰分析による傾きと y 切片の検定

Excel分析ツールによる回帰分析

これは上述の分析結果と同じである。

6.2. 係数と定数項がゼロ以外の場合に対する検定

これまで述べたように，回帰係数や定数項を検定する場合，教科書やウェブページでは，それらが 0 である場合の検定が説明されることが多い。しかしながら実際には，0 以外の任意の係数や定数項に対して検定可能である。係数や定数項 0 に対して検定可能ならば，一般性を失うことなく，任意の係数や定数項に対して検定可能であることは，意外と理解されていないらしい。この問題に関しては，次のページ参照：
回帰係数0とパラメータ0は検定が違う：黒木氏の非線形問題

統計解析ソフト R を用いて，任意の係数や定数項の検定を行なう場合，線形回帰であろうが非線形回帰であろうが， nls 関数を使えば良い。

7．回帰分析とは

前章で述べたことは回帰分析の一部とも言える。しかしながら，通常，回帰分析と言うと，回帰を利用した分散分析のことである。ここでは，その内容を見よう。

既に述べてきたことから察しがつくかもしれないが，データの y 方向への全変動 Sy は，回帰による y 方向への変動 Sr と誤差変動（残差平方和） Se の和であると考えることができる。

すなわち

\begin{align} Sy = Sr + Se \tag{22} \end{align}

ただし，ここで言う誤差変動とは，単に測定誤差の意味だけでなく，一次回帰式の x 以外の要因も含んでいる。

これらは，それぞれ式 (13), (10), (16) より，

\begin{align} Sy &= \sum (y - m_y)^2 \\ Sy &= \sum (Y - m_y)^2 \\ Sy &= \sum (y - Y)^2 \end{align}

ここで改めて， y は測定値， Y は回帰式 \(ax + b \) による計算値， \(m_y\) は測定値 y の平均であることに注意しよう。いずれも y 方向の値のみを問題としていて，最小二乗回帰の特徴が，ここにも現れている。

では具体的に，第 5 章で求めた式 (15) の回帰直線の回帰分析を行ってみよう。

\begin{align} y = 3.9024x + 35.122 \tag{15} \end{align}

これまでと重複した計算があるが，分かりやすくするため，それも含めて以下に Excel の計算方法を記述する。

データ y の平均： \(m_y\) = 80
傾きパラメータ： a = 3.9024
y 切片パラメータ： b = 35.122

表 4. データの集計方法

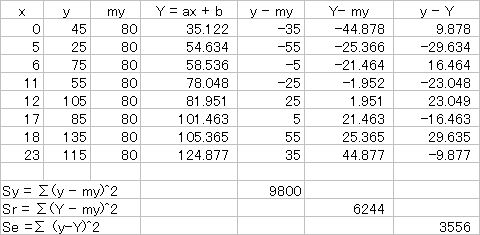
回帰分析データの集計法

式 (22) で述べたとおり，

\begin{align} Sy = Sr + Se \tag{22} \end{align}

となっている。

回帰分析の検定を行う前に，まず自由度を考えると次のようになる。

\begin{align} 回帰の自由度 DFr &= 説明変数 x の数 \\ &= 1 \\ 残差の自由度 DFe &= 標本サイズ n - パラメータ数 \\ &= 8 - 2 \\ &= 6 \\ 全体の自由度 DFy &= 標本サイズ n - 平均を求めたことによる1 \\ &= 8 - 1 \\ &= 7 \end{align}

当然だが，

\begin{align} DFy = DFr +DFe \end{align}

次に，全分散 Vy, 回帰分散 Vr, 残差分散 Ve を以下のように考える。

\begin{align} V_y &= \frac{S_y}{DF_y} \\ 　&= \frac{9800}{7} \\ 　&= 1400 \\ V_r &= \frac{Sr}{DFr} \\ 　&= \frac{6244}{1} \\ 　&= 6244 \\ V_e &= \frac{Se}{DFe} \\ 　&= \frac{3556}{6} \\ 　&= 592.67 \end{align}

このなかで，回帰分散 Vr と残差分散 Ve の比に対して F 検定を行うと回帰分析である。

\begin{align} F &= \frac{Vr}{Ve} \\ 　&= \frac{6244}{592.67} \\ 　&= 10.5 \end{align}

自由度（1, 6）に対して，p = 0.018

一方で， Excel を用いる回帰分析は，

ツール　→　分析ツール　→　回帰分析

とたどって，与えられたデータ \( (x, y) \) を分析した結果は以下の通りである。

表 5. EXCEL 分析ツールの回帰分析の分散分析

Excel分析ツールによる回帰分析

これは上述の分析結果と同じである。

以下の表 6 に， Excel 分析ツールによる回帰分析の全体像を示した。なお，傾きや切片の上下限 95％の部分は省略した。

表 6. EXCEL分析ツールの回帰分析表のまとめ。傾きや切片の上下限95％の部分は省略

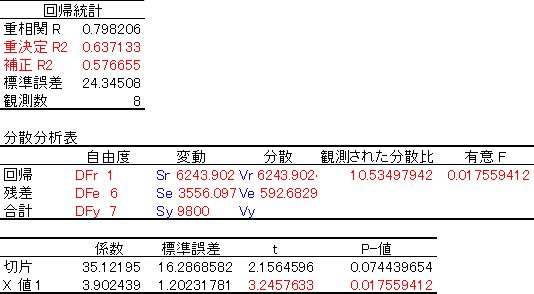
Excel分析ツールによる回帰分析

ここで，いくつか注意点を述べたい。

まず，決定係数 R² （重決定 R²）の定義は，回帰変動と合計変動の比である。

\begin{align} R^2 &= \frac{Sr}{Sy} \\ 　&= \frac{6243.902}{9800} \\ 　&= 0.637133 \end{align}

ただし繰り返し注意するが，既に第 4 章で述べたように，決定係数 R² には複数の定義が存在する。ここでは， Excel 分析ツールによる回帰分析の定義，すなわち，相関係数の 2 乗となる決定係数について解説していることを念頭に置いてほしい。

また，補正 R² は自由度調整済み決定係数 R*² とも呼ばれ，その定義は，残差変動と合計変動を，それぞれ自由度で割ったものの比を 1 から引いたもの，すなわち，残差分散と合計分散の比を１から引いたものである。

\begin{align} R^2 &= 1 - \frac{ \frac{S_e}{DF_e} } {\frac{S_y}{DF_y} } \\ &= 1 - \frac{V_e}{V_y} \\ 　&= 1 - \frac{592.6829}{\frac{9800}{7}} \\ 　&= 0.576655 \end{align}

ここで注意したいのは，Excel の結果が示す表には，不親切にも，

合計分散 = 合計変動 / 合計自由度
すなわち

\begin{align} V_y = \frac{S_y}{DF_y} \end{align}

が示されていないことである。

また，この自由度調整済み決定係数 R*² は，　Excel　でバグが出る場合があるので注意が必要である。この件は，以下のページ参照。

Excel 回帰分析のバグ？定数項なしの補正 R2

最後に，観測された分散比は，X 値 1 （傾き）の t 値の 2 乗であることに注意しよう。すなわち，
10.53497942 = 3.2457633²

これは，自由度 (1, n) の F 検定は，自由度 n の t 検定に等しいからである。当然，確率 p も等しく， 0.017559 となっている。

8. おわりに

粕谷 (1998) は，生物統計の入門書の中で，最小二乗法がｙ軸方向の距離のみを最小とするように計算されていることを知らないのは，｢恥だ」と述べている。しかし実際には，そのような人も多いのではないかと思う。

また，2 変数のグラフを書くときに，それをy 軸方向に拡大させて，ことさら変化を強調する方法を，Huff (1954) は「針小棒大法」と皮肉ったが，私も同意見である。

パソコンや，そのソフトが普及し，誰でもデータ分析できるようになってきた。しかし，少なくとも，自分が実行しようとしているデータ分析法や検定法の数学的背景も学習してほしいと思っている。そうしないと，分析結果の解釈やグラフ化の過程で，誤った適用や解釈が出てきても，本人は全く気づかないでいる，という困った例も増えてくるのではないかと危惧している。

参考文献

Huff D. (1954) How to lie with statistics.（統計でウソをつく方法，高木秀玄・訳, 1968）ブルーバックス，講談社.

粕谷英一 (1998) 生物学を学ぶ人のための統計のはなし. 文一総合出版.

（注 1）

決定係数 R² は，パラメータに関して線形結合である場合，つまり線形モデルであることを仮定しており，非線形モデルの適合度は正しく評価できない。しかしながら，それでもなお誤解（誤用？）して使う人が多いようである。それに関しては，次のページも参照：
Excelグラフ累乗，指数，多項式近似の論文記載の注意

さらに，学術論文でそれを指摘したものも参照して欲しい。
Spiess and Neumeyer (2010)
An evaluation of R2 as an inadequate measure for nonlinear models in pharmacological and biochemical research: a Monte Carlo approach
BMC Pharmacology 10:6

この論文の第１ページで，非線形回帰では，全変動が回帰変動と残差変動の和にならない，ことを指摘している。

（注 2）

UCLA の The Institute for Digital Research and Education (IDRE) は
What are pseudo R-squareds?
で，線形回帰における決定係数 R² に類似したモデル適合度指標（goodness-of-fit measure）として，非常に多くの偽 R2 (Pseudo-R2) と呼ばれる指標を紹介している。

（注 3）

回帰直線の傾き 0 の検定と，相関係数 0 （無相関）の検定が同等な自由度 n - 2 の t 検定であることは，以下のようにして示すことができる。

まず，回帰直線の傾き a を表す式 (4) を取り上げる。

\begin{equation} a=\frac{\sum (x-m_x)(y-m_y)}{\sum (x-m_x)^2} \tag{4} \end{equation}

次に，この傾き a を持つ回帰直線が平均値（重心）を通ることを示した式 (6) を考える。

\begin{equation} y = a(x - m_x) + m_y \tag{6} \end{equation}

これが，式 (17) 残差分散 Ve の中の計算値（予測値） Y となるので，結局，Ve は以下のようになる。

\begin{equation} V_e= \frac{\sum (y-a(x-m_x)-m_y)^2}{n-2} \end{equation}

この分子を展開すると

\begin{equation} V_e= \frac{\sum (y-m_y)^2 - 2a \sum (x-m_x)(y-m_y) + a^2 \sum (x-m_x)^2}{n-2} \end{equation}

さらに，式 (18) より，傾きの標準誤差 Sa は以下のようになる。

\begin{align} S_a = \sqrt{\frac{V_e}{\sum (x-m_x)^2}} \tag{18} \end{align}

その上で，
帰無仮説：傾き a = 0
の検定統計量 t は以下のようになる。

\begin{align} t = \frac{a}{S_a} \end{align}

さらに説明を続けるが，以上の式は煩雑なので，x，y の偏差を，それぞれ X，Y と置き換える。すると，以下のようになる。

\begin{align} &a = \frac{\sum XY}{\sum X^2} \\ &V_e= \frac{\sum Y^2 - 2a \sum XY + a^2 \sum X^2}{n-2} \\ &S_a = \sqrt{\frac{V_e}{\sum X^2}} \end{align}

ここで a を Ve に代入して整理する。

\begin{align} &V_e= \frac{\sum Y^2 - \frac{(\sum XY)^2}{\sum X^2}}{n-2} \end{align}

この残差分散 Ve を標準誤差 Sa に代入して整理する。

\begin{align} &S_a = \sqrt{\frac{\sum X^2 \sum Y^2 - (\sum XY)^2}{(n-2) (\sum X^2)^2}} \end{align}

この標準誤差 Sa と傾き a を，検定統計量 t の式に代入して整理する。

\begin{align} t &= \frac{\frac{\sum XY}{\sum X^2}}{\sqrt{\frac{\sum X^2 \sum Y^2 - (\sum XY)^2}{(n-2) (\sum X^2)^2}}} \\\\ &= \frac{\sqrt{n-2} \sum XY}{\sqrt{\sum X^2 \sum Y^2 - (\sum XY)^2}} \\\\ &= \sqrt{n-2} \frac{\sum XY}{\sqrt{\sum X^2 \sum Y^2 - (\sum XY)^2}} \end{align}

ここで式 (7) より，相関係数 r は以下のように定義される。

\begin{align} r = \frac{\sum XY}{\sqrt{\sum X^2 \sum Y^2}} \end{align}

この相関係数 r を，検定統計量 t に代入すると

\begin{align} t &= \sqrt{n-2} \: r \: \frac{1}{\sqrt{1 - r^2}} \\ &= \frac{r \sqrt{n - 2}}{\sqrt{1 - r^2}} \end{align}

これが，相関係数 0 （無相関）の検定統計量となる t 値の計算式である。つまり，回帰直線の傾き 0 に対する検定と，相関係数 0 に対する検定は，全く同じ自由度 n - 2 の t 検定なのである。

Home