logo
生物科学研究所 井口研究室
Laboratory of Biology, Okaya, Nagano, Japan
Home

回帰係数0とパラメータ0は検定が違う：黒木氏の非線形問題

井口豊（生物科学研究所，長野県岡谷市）
最終更新：2024 年 4 月 24 日

回帰係数が 0 でない場合の仮説検定を解説する。

偶然，ネット上で，以下のような非線形回帰の係数の統計学的検定に関する質問を見つけた。

その質問の中で，特に，気になったスレッドが， No.01788 2006/12/06(Wed) 18:09。統計解析ソフト R を使った非線形回帰分析の方法が回答された後，質問者・黒木氏が，仮説を"回帰係数(パラメータ)の値が 0 であるかどうか"としか置けないところが難点です，述べたことである。

黒木氏は，回帰係数（regression coefficient）とパラメータ（parameter）を同一視してしまっている，あるいは，混同している。しかも，それゆえ，値が 0 であるかどうかとしか置けない，と誤解してしまっている。両者は，もちろん異なるものであり，回帰分析で任意の実数の回帰係数の検定可能である。

実は，統計ソフト R の非線形回帰分析などでは，厳密に言うと，係数の検定を行なっているのではなく，パラメータの検定を行なっているのである。

例えば， a， b を定数として，以下のような直線を考える。

\begin{eqnarray} y=ax+b \end{eqnarray}

このとき， a は傾きを表す係数であり，かつ，パラメータである。統計ソフトでは，以下のような帰無仮説に対して検定される。

\begin{eqnarray} H_0\colon a=0 \end{eqnarray}

しかし，ここで p を定数として，例えば，次のように置いてみる。

\begin{eqnarray} a=p+1 \end{eqnarray}

すると回帰直線は，以下のようになる。

\begin{eqnarray} y=(p+1)x+b \end{eqnarray}

このとき，パラメータは p であるが，回帰係数は p+1 である。前述のとおり， R の非線形回帰分析などでは，パラメータの検定を行なうので，帰無仮説も以下のように変換される。

\begin{eqnarray} H_0\colon p=0 \end{eqnarray}

つまり，これは回帰係数に対して，以下のような帰無仮説の検定なのである。

\begin{eqnarray} H_0\colon a=1 \end{eqnarray}

実際に，以下のような x， y データを R で検定してみよう。 

x<- c(1, 2, 3, 4, 5)
y<- c(0, 3, 2, 6, 5)

line1<- lm(y~x)
(reg1<- summary(line1))  # 回帰分析

plot(x, y)
abline(line1, col="red")

まず，ここまでで，データの散布図（Scatter Diagram）と回帰直線が描ける。

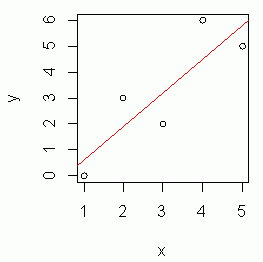
分析データの散布図と回帰直線

回帰係数の検定理論は，次のページ参照する。

特に，6. 回帰の検定に書かれている。

例えば，傾きを a，傾きの標準誤差を Sa，としたとき，傾きが 2 となるか否か，以下の帰無仮説のもとで検定する。

\begin{eqnarray} H_0\colon a=2 \end{eqnarray}

検定統計量 t は以下のようになる。

\begin{eqnarray} t=\frac{|a-2|}{S_a} \end{eqnarray}

ただし一般的には，傾きが 0 かどうか検定するので，以下のような帰無仮説と統計量で説明されることが多い。

\begin{eqnarray} H_0\colon a=0 \end{eqnarray}
\begin{eqnarray} t=\frac{|a-0|}{S_a} \end{eqnarray}

すなわち

\begin{eqnarray} t=\frac{|a|}{S_a} \end{eqnarray}

これが，黒木氏が，仮説を回帰係数(パラメータ)の値が 0 であるかどうかとしか置けないところが難点として参照したウェブページ偏回帰係数の検定が表す式である。

しかし，式を見てわかるとおり，回帰係数の値が 0 であるかどうかが検定できれば，一般性を失うことなく任意の係数について検定できるのである。これは， t 統計量が母平均の差の検定に用いられるように，差の検定に使われる統計量だということからも推察される。このような理論的な部分を，少なくとも，このスレッドを書いた時点では，黒木氏は見落としていたようである。

話を元に戻して，改めて以下の帰無仮説を，前述の定義式で R を使い検定する。

\begin{eqnarray} H_0\colon a=2 \end{eqnarray}

傾きとその標準誤差は，回帰分析の結果で，要素 coefficients の 2 行 1 列， 2 行 2 列のデータとして格納されているので，それを取り出して使う。 

a<- reg1$coefficients[2, 1]  # 傾き
sa<- reg1$coefficients[2, 2]  # 傾きの標準誤差

df<- length(x)-2  # 自由度
(tval<- abs(a-2)/sa)  # t 値
pt(tval, df, lower=F)*2  # p 値

結果は以下の通り。

t = 1.578457
p = 0.212573

しかし，これも以下のようにしてパラメータを検定すれば簡単である。

\begin{eqnarray} y=(p+2)x+b \end{eqnarray}

この場合は， nls 関数を用いる。これを非線形回帰の関数として解説している人もいるが，それだけではないのである。以下が，これを用いた検定のスクリプトである。 

line2<- nls(y~ (p+2)*x + b, start=c(p=1 ,b=1))
(reg2<- summary(line2))  # 回帰分析

reg2$coefficients[1, 3] # t 値
reg2$coefficients[1, 4] # p 値

実に簡単である。結果は以下の通り。

t = 1.578457
p = 0.212573

この結果は，当然だが，前述のように定義に従って計算した結果と同じである。

ここでは直線回帰（linear regression）を取り上げたが， nls 関数を使っているので，もちろん，非線形回帰（non-linear regression）において，係数が 0 でない場合の検定も出来る。

余談であるが，統計学における母数とは，パラメータ（parameter）のことであり，母平均とか母分散と言う時の，母である。その意味で， R は係数の検定ではなく，母数の検定を行なっているのである。

統計学における母数の意味を知らない人（大学教員も？）がかなり多い。それに関しては，次のページ参照してほしい。

Home