logo
生物科学研究所 井口研究室
Laboratory of Biology, Okaya, Nagano, Japan
Home

決定係数 R2 の違い: Excel, OpenOffice, LibreOffice および統計解析ソフト R を用いて

井口豊（生物科学研究所，長野県岡谷市）
最終更新： 2024 年 8 月 21 日

本ウェブサイトの解説は，以下の論文に引用されている。

鎌田敏之 (2015)
「データの活用」を育む表計算ソフトウェア活用学習とその実践
愛知教育大学技術教育研究 1: 23-28.

（注）ただし，この鎌田敏之 (2015)が引用しているのは，旧サイトの URL である。

稲田裕・米山一幸・加藤雅裕 (2022)
道路ネットワーク評価と道路診断を連動したインフラマネジメント手法の提案
インフラメンテナンス実践研究論文集 1(1): 471-480.

Excel における補正 R2 (自由度調整済み決定係数) の問題点は，以下のページを参照してほしい。

1. 原点通過（定数項 y 切片ゼロ）の直線回帰における決定係数とは

まず断っておくが,ここで扱うのは線形回帰の問題であり，ロジスティック回帰を含む非線形回帰に対しては，類似の指標として，擬似決定係数（pseudo R2）が使われることがある。それに関しては，以下のページを参照してほしい。

そのページでも解説したが， Excel 回帰直線の原点通過 （y 切片 0） グラフで，負の決定係数 R2 が表示されることがある。決定係数は寄与率とも呼ばれ，目的変数（従属変数） y の全変動に対する回帰変動の割合，すなわち，回帰式の適合度とも解釈される。それゆえ，マイナスになることは，一見おかしな結果である。しかしながら，実際には Kvalseth (1985) によれば，少なくとも 8 種類の異なる決定係数 R2 があり，しかもその違いに利用者が気づいてない。この定義の中には，場合によっては決定係数が負になるものもある。

ここでは，青木繁伸氏が Excel のバグとして紹介した以下の表 1 のデータを取り上げて，原点通過（y 切片 0）回帰直線の決定係数に関して，以下三つのソフトの計算結果を比較検討してみた。

なお当然ながら，ソフトのバージョンが異なると，使われる決定係数の定義も異なり，以下に示した結果通りにはならない場合もありうる。それは，それでまた困ったものだが・・。

表 1
x y
11
22
32
44
53
63
72
82
93
104

2. Excel の決定係数

x と y のデータを，次の表 2 のように， A2 - A11 と B2 - B11 のセルに入力したとする。

表 2

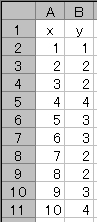
Data from Aoki

まず， Excel グラフを用いて決定係数を表すと，次の図 1 のようになる。

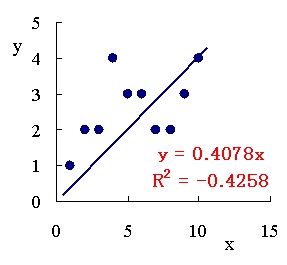
Excel 回帰直線グラフ

図1. y 切片無し（定数項ゼロ）の直線回帰.

一方， LINEST 関数を用いても，決定係数を求めることができる。ただし， LINEST 関数は，配列型の結果を返すので，その中から決定係数のみ取り出すならば， INDEX 関数を使って， 3 行 1 列目の要素として，それを取り出す。

= INDEX(LINEST(B2:B11, A2:A11, 0, 1), 3, 1)

0.8424

もちろん関数の使い方が面倒なら， LINEST 関数だけ使い，配列要素全てを見ると良い。しかしながら，特定の数値結果を転用するときに役立つので，このような数値の取り出し方も是非覚えておくべきである。

3. OpenOffice Calc の決定係数

OpenOffice Calc の，今回使用した ver. 3.3.0 では， Excel と異なり，グラフで原点通過の回帰直線を求めることはできない。したがって， LINEST 関数のみの利用となる。

=INDEX(LINEST(B2:B11; A2:A11; 0; 1); 3; 1)

0.2828

よく見ると分かるが， LINEST 関数の利用にあたって注意すべき点は， Excel では引数を ,（カンマ） で区切るのに対し， OpenOffice Calc では ; （セミコロン） で区切るということである。

4. 統計ソフト R の決定係数

統計ソフト R での，データ入力と，原点通過の直線回帰における決定係数の算出プログラムは以下の通りである。ここでは， lm 関数を用いて，通常最小二乗法（Ordinary Least Square, OLS）によって，回帰直線を求めた。

x<- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
y<- c(1, 2, 2, 4, 3, 3, 2, 2, 3, 4)
reg<- lm(formula = y ~ x-1)
summary(reg)$r.squared

0.8424

5. 決定係数の比較

以上の計算結果から，決定係数とピアソン積率相関係数（Pearson product-moment correlation coefficient）の 2 乗をまとめたのが，次の表 3 である。

表 3
決定係数 相関係数 2 乗
Excel グラフ -0.4258 0.2828
Excel Linest +0.8424 0.2828
Calc Linest +0.2828 0.2828
統計ソフト R +0.8424 0.2828

この表から，以下のことが容易に分かる。

それでは， Excel のグラフと Linest 関数，および統計ソフト R の決定係数は，どのように算出されるのだろうか？

それを明らかにするためには，まず回帰分散分析として，y 観測値を，以下のような 3 種類の変動として捉えてみることが必要になる。

全変動は回帰変動と残差変動の和になる。

\begin{align} TSS = RSS + SSR \end{align}

この中で，特に SSR と TSS に焦点を当てて，以下に解説する。

6. 残差平方和 SSR の算出

回帰直線の式自体は，どのソフトを使っても同じになるので， SSR も同じになる。すなわち，y の観測値 \(y_i \) と回帰による計算値（予測値） \(\hat{y}\) の差の 2 乗の和（平方和）である。

\begin{align} SSR = \sum (y_i - \hat{y})^2 \end{align}

6.1 Excel による SSR

Excel では， LINEST 関数が返す配列の中で， SSR は 5 行 2 列目にあるので，決定係数のとき同様， INDEX 関数を使って算出する。

= INDEX(LINEST(B2:B11,A2:A11,0,1),5,2)

11.9766

6.2 統計ソフトRによる SSR

sum(reg$residuals^2)

11.9766

7. 全平方和 TSS の算出

問題は，こちらの算出法である。

7.1 Excel グラフにおける TSS

\begin{align} TSS = \sum (y_i - \bar{y})^2 \end{align}

これは， Excel グラフ（図 1）では， TSS が y 観測値 \(y_i \) とその平均 \(\bar{y}\) の差の 2 乗和であることを意味する。

この値を求めるには， Excel の DEVSQ 関数を使えば良い。

=DEVSQ(B2:B11)

8.4

7.2 Excel の LINEST 関数における TSS

\begin{align} TSS = \sum y_i^2 \end{align}

LINEST 関数では， TSS が y 観測値の 2 乗和であることを意味する。

すなわち， Excel グラフでは， TSS の変動基準を y 平均値としているの対し， LINEST 関数では，それを y = 0 としている。

この値を求めるには， Excel の SUMSQ 関数を使えば良い。

=SUMSQ(C72:C81)

76

これは， LINEST 関数の配列要素を使って求めることもできる。すなわち， LINEST 関数 5 行 1 列に回帰平方和（RSS）， 5 行 2 列に残差平方和（SSR）があるので， TSS は両者の和として求めれば良い。

TSS = RSS + SSR
= INDEX(LINEST(B2:B11,A2:A11,0,1),5,1) + INDEX(LINEST(B2:B11,A2:A11,0,1),5,2)

76

7.3 統計ソフト R における TSS

\begin{align} TSS = \sum y_i^2 \end{align}

統計ソフト R も， LINEST 関数と同じく，TSS が y 観測値の 2 乗和であることを意味する。

TSS を具体的に求めるには，最小二乗法による直線回帰の結果に対し，分散分析（ANOVA）を行うと，平方和を表す Sum の 1 列目に回帰平方和 RSS， 2 列目に残差平方和 SSR があるので， TSS は両者の和として求めれば良い。

anova(reg)$Sum[1]+anova(reg)$Sum[2]

76

8. 決定係数 R2 (R-Squared) の算出

前述のことから推察できるだろうが，実は， Excel グラフも，　Excel の LINEST 関数も，そして統計ソフト R も，基本的には，決定係数に同じ式を使っている。すなわち，

\begin{align} R^2 = 1 - \frac{SSR}{TSS} \end{align}

この式で，全変動 TSS の定義が異なるために，異なる R2 が算出されるのである。

以下に， Excel グラフ， LINEST 関数，統計ソフト R における決定係数の算出法を示すとともに，それぞれが， Kvalseth (1985) が紹介した 8 種類の異なる決定係数の定義の中で， R21 と R27 に当たることも示した。

Excel graph:
\begin{align} R^2_1 &= 1 - \frac{\sum (y_i - \hat{y})^2}{\sum (y_i - \bar{y})^2} \\ &= -0.4258 \end{align}
Excel LINEST, Software R:
\begin{align} R^2_7 &= 1 - \frac{\sum (y_i - \hat{y})^2}{\sum y_i^2} \\ &= 0.8424 \end{align}

なお， 表 3 に示した OpenOffice calc の決定係数，すなわち相関係数の 2 乗という定義は， Kvalseth (1985) の R25 に相当する。

OpenOffice calc は， Excel との互換性を追及しているはずだが，決定係数の算出に関して，なぜか全く異なる定義を採用している。

一方， LibreOffice で LINEST関数から算出される決定係数は， Excel のそれと同じく R27 である。

また，医療統計解析ソフトウェア GraphPad Prism では，原点通過（y 切片ゼロ，定数項なし）の回帰直線に対して，デフォルトでは決定係数を表示しない。解説書 Prism v5 Regression Guide の p.41, Why Prism doesn't report r2 in constrained linear regression において， R21 と R27 の定義を挙げ，どちらも問題点があることを指摘している。この点は確かにその通りであり，後述するような問題点が両者に現れる。

それでも Prism でこの決定係数を求めたい場合は，非線形回帰のオプションで求めるようになっている。その場合， Prism も Excel グラフと同じく R21 を使うので，負の決定係数が出てくる。

また，古生物学や生態学の分野では有名なフリーの表計算・統計分析ソフト PAST では，原点通過直線の決定係数で， 相関の 2 乗となる定義 R25 を採用している。

ソフトごとの決定係数の定義をきちんと知り，自分でその定義式を使って算出してみないと，単純にプログラムエラーだと思ってしまうので注意が必要である。

余談だが， PAST は， Excel のようなセルにデータを入力し，ヒストグラムや散布図も出力でき，かつ，数十種類の統計分析ができる優れたフリーソフトである。しかも，インストールせずに，実行ファイルをクリックするだけで使えるので，非常に動作が軽快である。

9. Excel グラフなどの決定係数 R21 (R-Squared 1) は不適切か？

前述のとおり，歴史的には少なくとも 8 種類の異なる決定係数が用いられてきたのである（Kvalseth, 1985）。だから，原点通過（定数項無し）の直線回帰モデルに対して， R21 の定義は間違いだ，と単純には言えない。

例えば， 私が「 決定係数 R2 の誤解」で扱ったデータに回帰直線を当てはめてみる。

表 4
x y
1030
2010
3030
4050
5030
6060
7090
80110
9090
100110

実は，これは，回帰直線が原点を通過するように意図的に作られたデータなのである。

すなわち，以下のように，定数項有り (1) と，定数項無し (2) で，回帰式が完全に一致する。

回帰モデル 1 （定数項あり）

\begin{align} y = 1.109 x + 0 \end{align}

回帰モデル 2 （定数項なし）

\begin{align} y = 1.109 x \end{align}

ここで， Excel グラフを利用すると，どちらにも R21 を使うので，両者の決定係数もまた一致する。

回帰モデル 1
R2 = 0.8394

回帰モデル 2
R2 = 0.8394

ところが，統計ソフト R では，原点通過するかどうか，つまり，定数項の有無で，異なる定義の決定係数を使うので，両者の決定係数は異なってしまうのである。

回帰モデル 1
R2 = 0.8394

回帰モデル 2
R2 = 0.9606

つまり，統計ソフト R では，全く同じ回帰直線が得られたとしても，原点通過するかどうか，つまり，定数項の有無で，それぞれ R21 と R27 を使い分けるので，決定係数が異なってしまうのである。

もちろん，推定したパラメータ数は，定数項有りでは a と b の二つ，定数項無しでは a の一つと異なるので，自由度を補正した決定係数ならば，それが両者で異なるのが当然である。しかし，ここで問題にしているのは，その補正をしない，通常の決定係数なのである。

以上の計算例を見れば， Excel グラフの決定係数が不適切と一概には言えないのである。もちろん，バグではない。

10. 本質的な問題は何か？

ここまでの問題は，原点通過の回帰直線を考える時，決定係数が負になるような定義 R21 は不適切なのか，という点であった。しかしながら，この問題が取り上げられるとき，多くの場合，そもそも原点通過モデルを設定するのが正しいのか，という議論が，すっぽり抜け落ちているのである。これこそ，むしろ本質的に重要な問題なのである。

この点をまさに突いているのが， Motulsky and Christopoulos (2003) による p. 35 の指摘である。

R2 will be negative when the best-fit curve fits the data worse than a horizontal line at the mean Y value. This could happenn if you pick an inappropriate model.

逆に言えば，決定係数が負になることも承知の上で，定義 R21 が使われることを示している。

最初に示したデータ（表 1）を実際に検討してみよう。それには，定数項有りのモデルを考えて，定数項がゼロである，という帰無仮説を検定すれば良い。

厳密に言えば， b は標本の傾きであり，検定は推定された母集団の定数項に対して行われるのであるが，ここでは，そういった表現上の厳密さは問題にしない。

統計ソフト R を使えば，以下のようなプログラムになる。

x<- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
y<- c(1, 2, 2, 4, 3, 3, 2, 2, 3, 4)
reg<- lm(formula = y ~ x)
summary(reg)$coefficients

その結果を次の表 5 に示す。

表 5
Estimate Pr(>|t|)
Intercept 1.666667 0.02279009
x 0.169697 0.11360499

定数項は有意にゼロと異なる。すなわち，表 1 データの場合，元々，原点を通過しない，定数項ゼロとは言えない回帰直線を，強制的に原点通過させて論じているのである。まさに，前述の Motulsky and Christopoulos (2003) の指摘どおりの結果なのである。

決定係数が負になるのは変だ，と言う以前に，それがどのような条件下で起こるのか，という本質的に重要な問題が，ここに存在する。

さらに，次の表 6 のデータを考えてみよう。

表 6
x y
110180
120170
130180
140170
150160
160160
170150
180145
190140
200145

Excel グラフを用いて決定係数を表すと，次の図 2 のようになる。

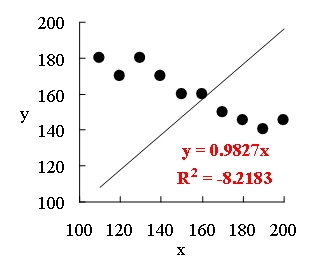
表5データに対するy切片無し（定数項ゼロ）の直線回帰

図 2. 表 6 データに対する y 切片無し（定数項ゼロ）の直線回帰.

Excel グラフの決定係数は，負になるどころか，絶対値 1 を大きく上回るのである。

一方，統計ソフト R を用いて，このデータに対する y 切片無しの回帰直線の決定係数を求めてみる。

x<- c(110, 120, 130, 140, 150, 160, 170, 180, 190, 200)
y<- c(180, 170, 180, 170, 160, 160, 150, 145, 140, 145)
reg<- lm(formula = y ~ x-1)
summary(reg)$r.squared

0.9303

なんと，統計ソフト R の決定係数では，この y 切片無しの回帰直線は非常に良く適合している，という結果が出るのである。

こんなデータに y 切片無しのモデルは考えない，と言うかもしれない。しかしそれを言うなら，前述のように， y 切片がゼロとは有意に異なる表 1 データに， y 切片ゼロのモデルを適用したことと，五十歩百歩の議論である。

もう一度， Motulsky and Christopoulos (2003) の指摘を思い出してみよう。 Excel グラフの決定係数の定義，すなわち R21 が，負になるのは不適当なモデルを選んだときだ，と言うのである。その意味からすれば，表 6 のデータに対して， R21 がマイナス 8 にもなったのは，より不適当なモデルだからこそなのである。

つまり，負の決定係数は当てはまりの悪さの指標，と言えるのである。

いずれにせよ，決定係数に複数の定義があることは事実であり，それぞれ一長一短の性質を持つと言える。その考察なしに，負の決定係数が出る，というだけで，そのプログラムを正しくないとか，バグであるとか結論するのは，拙速だと言えよう。

補遺 1

表 1 のデータと表 6 のデータに対して，定数項ありの回帰直線モデルと定数項なし（y 切片ゼロ，原点通過）の回帰直線モデルの適合度を，以下のようにして調べてみた。

前述のように，両者では推定されたパラメータの数が異なるので，決定係数 R2 でなく，補正済み（自由度調整済み）決定係数 R*2 (adjusted R-squared) と赤池情報量規準 AIC (Akaike Information Criterion)を用いて，適合度を評価した。 AIC に関しては，補遺 2 も参照して欲しい。

統計ソフト R で AIC を算出する時は，例えば， x, y データに対して，以下のようにすれば良い。

reg<- lm(formula = y ~ x)
AIC(reg)

まず，表 1 のデータに対して，定数項有りの回帰直線と，定数項なし（y 切片ゼロ，原点通過）の回帰直線を当てはめたグラフが次の図 3 であり，その分析結果が，その下の表 7 である。

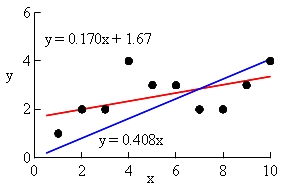
定数項の有無による回帰式の違い

図 3. 表 1 データに対する定数項有りと無しの回帰直線の当てはめ.

表 7
y = 0.408 x y = 0.170 x + 1.67
Excel グラフの R*2 −0.604 +0.193
統計ソフト R の R*2 +0.825 +0.193
AIC 34 29

ここで注意すべきは以下の点である。

すると， AIC によれば，定数項ありのモデルのほうが適合度が高い，と言える。これは， Excel グラフの R*2 でも同じ結論である。

しかしながら，統計ソフト R の R*2 では，定数項なしのモデルのほうが，かなり適合度が高いという結果が出る。

つまり，定数項の有無のモデル間で適合度を比較すると，奇妙な結果を出すのは，むしろ統計ソフト R のほうである。 SPSS も統計ソフト R と同じ定義の決定係数を利用するので， Excel グラフよりも，統計ソフト R や SPSS のほうが奇妙な結果になると言える。

これは，表 6 のデータについて，次のグラフ（図 4）と分析結果（表 8） を見ると，もっとはっきりする。

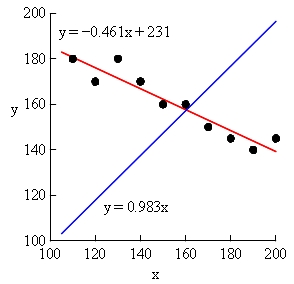
Comparison of fit between the linear regressions with and without an intercept.

図 4. 表 6 データに対する定数項有りと無しの回帰直線の当てはめ.

表 8
y = 0.983 x y = −0.461 x + 231
Excel グラフの R*2 −9.37 +0.885
統計ソフト R の R*2 +0.923 +0.885
AIC 107 64

図 4 を見れば，どちらが適合度が高いか，分析するまでもなく，一目瞭然だろう。

表 8 から，確かに， AIC と Excel グラフの R*2 では，定数項ありのモデルのほうが適合度が高い，と分かる。ところが，統計ソフト R では，定数項なしのモデルのほうが，適合度が高いのである。

この例でもまた，Excel グラフよりも，むしろ，統計ソフト R や SPSS のほうが奇妙な結果を出すと言える。

もちろん，あらゆるデータで，このような傾向が認められるとは限らない。しかし少なくとも， Excel グラフでは決定係数がマイナスになるから正しくない，という意見は短絡的と言えるだろう。ましてや，それが修正が必要なバグとは単純には言えない。

では， Excel グラフの決定係数が正である場合はどうなのだろうか？

産総研の工藤祐揮氏が，かつてExcel のバグを確認してみるというページで示したデータを取り上げて調べてみよう。現在では，このページは存在しないが，決定係数の計算を考える上で，興味深いデータであるので，敢えてここで再掲する。小数点以下の細かい数字は省略してある。

表 9
x y
18759.6036
12406.1353
12205.2843
 8554.7610
 8254.2004

定数項ありの回帰直線と，定数項なし（y 切片ゼロ，原点通過）の回帰直線を当てはめたグラフが，次の図 5 である。

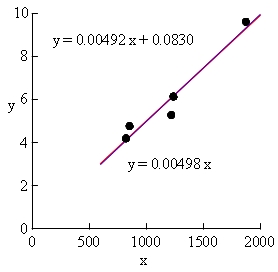
Comparison of fit between the linear regressions with and without an intercept.

図 5. 表 9 データに対する定数項有りと無しの回帰直線の当てはめ.

工藤氏が取り上げたデータでは，定数項ありの直線と定数なしの直線が，ほとんど一致し，この図では見分けがつかない。

まず次の表 10 で，通常の決定係数 R2 と残差平方和 SSR を見てみよう。

表 10
y = 0.00498 x y = 0.00492 x + 0.0830
Excel グラフの R2 +0.9475 +0.9477
統計ソフト R の R2 +0.995 +0.948
残差平方和 SSR 0.960 0.957

単純に考えると（自由度を考慮しないと），パラメータを増やせば適合度が良くなり，したがって，残差平方和 SSR は減少し，決定係数 R2 は大きくなる。

表 10 では，定数項ありの直線は，定数項なしの直線に比べて， SSR は，わずかながらではあるが確かに減少している。それに対応し， Excel グラフの R2，すなわち R21 も，わずかながら増加している。

ところが，統計ソフト R の R2，すなわち R2７ は減少してしまっているのである。ここでも，むしろExcel グラフの決定係数のほうが，自然な変化を示しているのである。

R2７ の奇妙な変化は，その全変動 TSS の定義が， y = 0 を基準としていることに由来する。つまり，この定義は，回帰式が原点を通る，ということだけに注目し，データがどのように分布しているかは十分考慮していないのである。

繰り返しになるが，決定係数には様々な定義，すなわち， Kvalseth (1985) によれば 8 種類もの定義がある。そのうち，原点通過（定数項なし， y 切片ゼロ）の回帰でどれを採用するかは，一意的に決められていない。その点を，工藤氏は見落としていたのかもしれない。

引き続き，工藤氏のデータで，今度は補正済み（自由度調整済み）決定係数 R*2 と AIC を調べてみる。前述の通り，パラメータを増やせば，残差 SSR が減少し，見かけ上は適合度が高くなる。そのパラメータ増加分を補償（補正）しようというのが， R*2 である。

表 11
y = 0.00498 x y = 0.00492 x + 0.0830
Excel グラフの R2 +0.934 +0.930
統計ソフト R の R2 +0.994 +0.930
AIC 9.9 11.9

Excel グラフ，統計ソフト R， AIC，いずれもが自由度を考慮すれば，原点通過（定数項なし，y 切片ゼロ）の回帰直線のほうが適合度が高い，という結果になる。

このデータの回帰分散分析の結果も見てみる。

表 12
Estimate Pr(>|t|)
Intercept 0.0830201 0.92760
x 0.0049160 0.00516

定数項は有意にゼロと異ならないことが分かり，定数項なしの回帰式の適合度が高いという表 11 の結果を支持する。

以上のことは，工藤氏のデータにおいても，Excel グラフの決定係数 R21 が，実用上問題無いことを示している。工藤氏は， R2７ は正しく， R21 は正しくない，と結論したが，その理論的根拠は示さなかった。

もちろん，定数項の有無で，異なる定義の決定係数を用いる場合は，それらを比較できない，と考えることも可能である。しかしそれなら，比較不可能な決定係数の意義は何だろうか，と考えてしまう。仮に，決定係数を単独で使うとしても，図 2 のような回帰直線の R2 を 0.9303 と高く出す統計ソフト R のような定義 R2７ が妥当なのかは疑問である。少なくとも， R2７ は正しく， R21 は正しくない，と単純には割り切れないであろう。

補遺 2

赤池情報量規準 AIC (Akaike's Information Criterion) は，故・赤池弘次が残した情報理論に関する，日本が世界に誇る業績である。しかしながら，大学で統計学を学んだ学生でも， AIC の理論や用法，さらには赤池のことを知らない人も多い。

統計数理研究所のウェブサイトには，赤池の業績を紹介した赤池記念館があるが，これもあまり知られていない。大学の統計学の授業では，少しでも良いので，赤池氏のことに是非触れて欲しいものだ。

赤池が， 2006 年に第 22 回京都賞を受賞したときのメッセージが YouTube に残されている。

以前，テレビ放送された放送大学「統計学」（藤井良宜）は，初歩的な科目ではあるが，第 １ 回の講義から AIC に触れ，赤池が京都賞を受賞したことにも触れていた。放送大学の講義内容には感心するものが多い。

なお，私が発表したクワガタムシの形態変異（三型）に関する論文（Igichi, 2013）でも，不連続・線形回帰モデルと連続・非線形回帰モデルの適合度の評価に， AIC を用いられている。

Wikipedia にも，赤池情報量規準の説明がある。この説明の中で， n を標本数と説明した部分があったので，標本サイズと訂正した。標本サイズは，多い少ないではなく，大きい小さいで形容する点も訂正した。

標本数と標本サイズは全く異なる用語であるが，しばしば混同されるし，この問題に関連して，以下のページも参照してほしい。

参考文献

Eisenhauer J. G. (2003)
Regression through the Origin
Teaching Statistics 25: 76-80.

Iguchi Y. (2013)
Male mandible trimorphism in the stag beetle Dorcus rectus (Coleoptera: Lucanidae)
European Journal of Entomology, 110: 159-163.

Kvalseth T. O. (1985)
Cautionary Note about R2
The American Statistician 39: 279-285.

Motulsky H. and Christopoulos A. (2003)
Fitting models to biological data using linear and nonlinear regression
GraphPad Software Inc., San Diego CA.

Home