決定係数R2の誤解：必ずしも相関の２乗という意味でなく，負にもなるし，非線形回帰には使えない

井口豊（生物科学研究所，長野県岡谷市）
最終更新：2024 年 8 月 21 日

タイトルにも書いたが， 2 乗と言っても，計算式が必ずしも 2 乗となるわけではなく，便宜上，決定係数 （coefficient of determination） あるいは寄与率と呼ばれる統計量を R² と表記するのである。その点をまず，きちんと理解しておいてほしい。この問題に関しては，次のページも参照してほしい。

• 決定係数 R² の違い: Excel, OpenOffice, LibreOffice および統計解析ソフト R を用いて

さらに， Excel における補正 R² （自由度調整済み決定係数）の問題点は，以下のページを参照してほしい。

• Excel 回帰分析のバグ？定数項なしの補正 R²

本ページの内容は，坂口（2017）によって引用され，さらに解説も加えられた。それも参照して欲しい。これを含めて，参考文献は最後に一括して挙げてある。

決定係数に関しては，「決定係数は相関係数の二乗だから負（マイナス）にならない」と説明されることがある。しかしこの説明は，二点で明らかに間違いである。まず第一に，決定係数には複数の定義が存在し，必ずしも相関係数の二乗とはならない。第二に，負にならない定義の決定係数であっても，それは相関係数の二乗とは限らないのである。

この点に関しては，統計学の基礎的な教科書をよく読んでほしい。「相関係数の二乗は，決定係数」と書かれることは，しばしばあるが，「決定係数は，相関係数の二乗」と書かれることは，ほとんどないはずである。正しく説明されている教科書ならば，後者のように説明されていないはずである。

ところが困ったことに，この決定係数と相関係数の関係をきちんと理解していない人が多いのである。大学教員や研究者にさえ，そのような人がいる。これは，決定係数に限ったことではないようで，鎌田 敏之（2015）によれば，理論に関心が薄い実践側の研究者が執筆した教科書やウェブ上の講義ノートには，明らかに誤った説明がされているものがあるそうだ。

前述の私のウェブページの補遺１で，定数項ありの回帰直線モデルと，定数項なし（y 切片ゼロ，原点通過）の回帰直線モデルの適合度を比較した。おかしな結果を出すのは Excel ではなく，むしろ統計ソフト R による決定係数であることを示した。

Kvalseth (1985) は， R² の定義として 8 種類挙げているが，このうち，原点通過（y 切片ゼロ，定数項なし）の回帰直線に対して，ソフトによって以下のような定義が使われる。ただし，バージョンによって変更があるかもしれない。

• R²-1・・・Excelグラフや医療統計解析ソフトウェアGraphPad Prism
• R²-5・・・OpenOffice Calcや生物・古生物統計ソフトPAST
• R²-7・・・Excelワークシート，LibreOffice LINEST 関数，統計ソフトR，SPSS

このうち，R²-1 は負の値も取る。 Prism では，原点通過回帰直線の R² は意味が曖昧という理由で，デフォルトでは R² を算出しない。 R²-1 と R²-7 の定義を挙げ，どちらも問題点があることを指摘している。あくまで決定係数を求めたい場合は，非線形回帰のオプションで求めるようになっている。その場合， R²-1 を使うので， Excel グラフと同じく，負の決定係数も出てくる。 GraphPad Curve Fitting Guide の p.189 には，わざわざ次のように書いてある。

R2 can be negative!

これは決定係数が負になることを承知の上で使う典型例である。

相関係数の二乗として定義されているのは， R²-5 である。「相関係数の二乗だから決定係数が負にならない」のではなく，「この定義を使えば，決定係数が負にならない」のである。

また，Excelとの互換性を追及しているはずの OpenOffice Calc で， Excel と異なる定義が使われるのは興味深い。一方で，同じくフリーのオフィスソフトである LibreOffice LINEST 関数では， Excel のワークシートと同じ計算が行われる。

R²-7 は負にならないが相関係数の二乗でもない。定義式を確認せずに，ソフトウエアだけを頼りにして，この R²-7 を算出して，これが相関係数の二乗だと思っている（思い込んでいる）人もいる。

統計ソフトによって原点通過の回帰直線の決定係数が異なる問題に関しては， Eisenhauer (2003) も指摘していて， R² の定義が複数存在することも述べている。決定係数のこのような定義の違いは，原点通過，定数項なし，つまり，切片ゼロの回帰直線での， R² を考えるときには，大きな問題となる。

ここでは以下のデータを使い，まず，相関係数と決定係数の関係を具体的に調べてみよう。

x: 1 2 3 4 5 6 7 8 9 10
y: 1 2 2 4 3 3 2 2 3 4

まず，相関係数およびその二乗を求める。EXCELなら，CORREL関数で求められるが，ここでは，統計解析ソフト R を使う。

### 相関係数と相関係数の二乗
x<- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
y<- c(1, 2, 2, 4, 3, 3, 2, 2, 3, 4)
cor(x, y)
cor(x, y)^2
####

相関係数と相関係数の二乗の結果は，それぞれ次のようになる。
0.531816
0.2828283

統計ソフト R では，原点通過の回帰式を求めると，決定係数 R² も算出される。この場合， lm 関数にオプション -1 を入れれば良い。

### 原点通過の回帰直線の決定係数
reg<- lm(formula = y ~ x-1)
summary(reg)
#######

結果は，次の通り。

R-squared: 0.8424

この場合，決定係数が相関係数の二乗とは，全く異なる数値だと分かる。つまり，決定係数は，必ずしも相関係数の二乗とは言えないのである。

次に，以下のデータを， EXCEL2003 を使って分析してみよう。これは，原点通過の回帰直線のグラフで，負の決定係数 R² が出てくるバージョンである。

x y
10 30
20 10
30 30
40 50
50 30
60 60
70 90
80 110
90 90
100 110

回帰直線のグラフで， y 切片有りと， y 切片無しで，比較したのが次の図である。

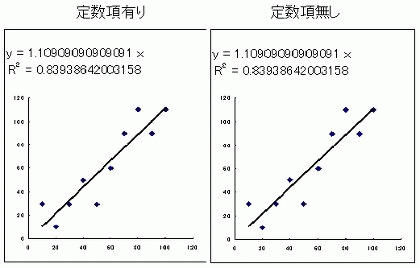
小数点以下14桁まで出しても，決定係数は同じ R² = 0.83938642003158

両方のグラフ自体が全く同じに見えるが，実は，このデータを使うと，定数項有りのモデルでも切片はゼロなのである数式処理ソフト Maxima を使うと簡単に確認できる。

/* 回帰式 */
M: matrix(
[10, 30],
[20, 10],
[30, 30],
[40, 50],
[50, 30],
[60, 60],
[70, 90],
[80, 110],
[90, 90],
[100, 110] );

lsquares_estimates (
M, [x,y], y = a*x+b, [a, b]);
/* 終了 */

結果は，次の通り。

Maxima では，パラメータが正確に分数で出力され，定数項もゼロと分かる。このデータを，統計ソフト R を使って，定数項有りの直線回帰を求めると，以下のようになる。

dat<- matrix(c(
10, 30,
20, 10,
30, 30,
40, 50,
50, 30,
60, 60,
70, 90,
80, 110,
90, 90,
100, 110
), ncol=2, byrow=T)

x<- dat[, 1]
y<- dat[, 2]

lm(y ~ x)

結果は，次のとおり。

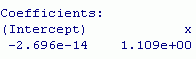
つまり， y 切片は完全にはゼロ表示されない。この意味で， Maxima のほうが正確な数値を返すと言える。

このデータを使って， EXCEL 分析ツールの回帰分析で計算すると，以下のようになる

Excel 分析ツールでは，両者は異なる。

一方， R を使って分析すると以下のようになる

やはり両者は異なり， R の結果は， EXCEL 分析ツールの結果と一致する。

EXCEL 分析ツールも R も，原点通過するかしないか，つまり， y 切片が有るか無いかで，決定係数 R² の定義が全く異なる。したがって，上図のように，同一データに対して， y 切片が有っても無くても同一の回帰式が得られ，同一の残差となる場合でも，決定係数は異なるという奇妙な状態も起きうるのである。

これは極端な例だが，元の式の y 切片がゼロに近いと， EXCEL や R では，切片ゼロのオプションにすると，決定係数 R² が極端に変化しすぎることを意味する。そして，このような場合は，むしろ，EXCEL グラフの決定係数 R² のほうが妥当であると思われる。 Motulsky and Christopoulos (2004) の p.35 では， R² が負になる定義を認めた上で，それは不適当なモデルを選んだときと説明しているが，私もそのような解釈に賛成である。

決定係数に関する誤解の二点目は，決定係数は線形モデルを仮定しており，非線形モデルの適合度評価には使えないということである。これも案外知られていない。例えば，煙草の問題を考えようというサイトの中の，統計情報の評価というページでも，「決定係数を使用すれば、非線形のモデル式を評価することができる」と誤った説明をしている。この点に関しては， Spiess and Neumeyer (2010) が，非線形回帰では，全変動が回帰変動と残差変動の和にならないことを指摘している。

なお，ロジスティック回帰を含む非線形回帰において，決定係数に類似の指標として，擬似決定係数（pseudo R²）が使われることがある（Hu et. el., 2006）。ただし，これも複数の定義があり，使いづらい指標である。それらの定義については，UCLA の解説ページ参照：
FAQ: WHAT ARE PSEUDO R-SQUAREDS?

回帰係数は二変量 X，Y が直線関係でなければ使えない，というのも誤った説明である。例えば，以下のようなデータを考えてみよう。

x y
1 5
2 1
3 15
4 10
5 30
6 28
7 60
8 58
9 85
10 110

これを次のような二次関数（放物線）で多項式（polynomial）近似してみる。

このような多項式はパラメータに関して線形であり，最小二乗法はパラメータを偏微分するので，線形回帰（linear regression）として扱える。曲線ならば非線形回帰というわけではないのである。したがって，多項式近似は，曲線となっても決定係数で評価できる。

まず，統計ソフト R を使い，相関係数の 2 乗と決定係数を比べてみる。

x<- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
y<- c(5, 1, 15, 10, 30, 28, 60, 58, 85, 110)
reg<- lm (formula = y ~ 1 + I(x^2))  # y=a*x^2 + b

cor(x,y)^2  #相関係数の2乗
summary(reg)$r.squared  #決定係数

結果は以下のとおり。

相関係数の2乗 0.8955722
決定係数 0.9675653・・（１）

相関係数の 2 乗は，このデータを EXCEL の CORREL 関数で求めて 2 乗しても同じである。つまり，相関係数の 2 乗と決定係数は， 2 次関数の場合は異なる。そして，グラフは次のようになる。

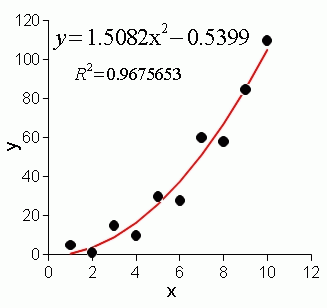
この決定係数を機械的に求めるには，まず x² のデータを計算する。

x x^2 y
1 1 5
2 4 1
3 9 15
4 16 10
5 25 30
6 36 28
7 49 60
8 64 58
9 81 85
10 100 110

ここで，次のように変数変換する。

その上で，次のような直線近似すれば良いのである。

R を使うならば，次のようにすれば良い。

dat<- matrix(c(
1, 5,
2, 1,
3, 15,
4, 10,
5, 30,
6, 28,
7, 60,
8, 58,
9, 85,
10, 110
), ncol=2, byrow=T)

x<- dat[, 1]
X<- x^2
y<- dat[, 2]

lm(y ~ X)

cor(X,y)^2  #相関係数の2乗
summary(reg)$r.squared  #決定係数

結果は，相関係数の 2 乗も，決定係数も 0.9675653，両者は一致し，前述の (1) の決定係数とも一致する。グラフは，次のようになる。先ほどのグラフの回帰式とパラメータが全く同じであると分かる。

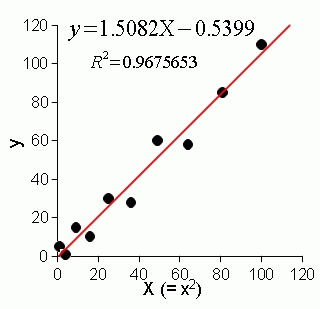
つまり，多項式回帰における決定係数とは，データ分布が直線になるように変数変換し，その回帰直線の相関係数の二乗を求めたことになる。

EXCEL で同様な分析をするなら， x² と y の直線回帰式を SLOPE 関数と INTERCEPT 関数で求め，決定係数もその変換データを使い， CORREL 関数の 2 乗値を求めれば良い。通常最小二乗法（Ordinary Least Square: OLS)では， y 軸方向の変動しか問題とならないため，このような x の変数変換が可能なわけである。

参考文献

Eisenhauer J. G. (2003)
Regression through the Origin
Teaching Statistics 25: 76–80.

Hu B., Shao J. and Palta M. (2006)
Pseudo-R2 in logistic Regression Model
Statistica Sinica 16: 847–860.

Kvalseth T. O. (1985)
Cautionary Note about R2
The American Statistician 39: 279-285

Motulsky H. and Christopoulos A. (2004)
Fitting models to biological data using linear and nonlinear regression
Oxford University Press

坂口栄一郎（2017）
研究発表での r2 の使用について思うこと
農業食料工学会誌 79(5): 383-384.

Spiess A. N. and Neumeyer N. (2010)
An evaluation of R2 as an inadequate measure for nonlinear models in pharmacological and biochemical research: a Monte Carlo approach
BMC Pharmacology 10:6