不偏標準偏差とは？：統計検定を理解せずに使っている人のために

井口豊（生物科学研究所，長野県岡谷市）
最終更新：2024 年 11 月 28 日

1. はじめに

統計学の用語について，誤解・誤用の例をこれまでも書いてきた。

ここで，もうひとつ気になるのが，「不偏標準偏差」という用語である。ここのページタイトルにも書いたが，池田（2013）の解説論文「統計検定を理解せずに使っている人のために II」を読むと，改めて，「不偏標準偏差」という表現の奇妙さが気になってしまった。

なお，池田（2013）は，「標本数」という用語を何度も使っているが，これは前述のとおり，明らかな誤用であり，「標本サイズ」が正しい。しかも彼は，標本数が「多い」「少ない」と形容しているが，サイズだから，「大きい」「小さい」と形容すべきであった。これは，大標本・小標本と言うが，多標本・少標本とは言わないことからも分かる。さらに，池田（2013）は，「n 個の標本」と何度も書いているが，これも「大きさ n の標本」と書くべきであった。「n 個の標本」では，文字通り，サンプル数が n という意味になってしまう。

本論に戻って，改めて，不偏標準偏差とは何かを考えて見よう。なお，このウェブサイトは，以下の論文で引用されている。

小西敬三・鳥居建史・木村範孝・小林広樹・岡田大輔（2023）
副室ジェット燃焼エンジンの高周波燃焼騒音発生メカニズム解析 (第 2 報) -燃焼室共鳴周波数帯の筒内圧力振動の評価法
自動車技術会論文集，54(5): 887-894.

2. 改めて，不偏標準偏差とは？

母標準偏差の不偏推定量としての「不偏標準偏差」の数学的証明は，例えば，統計ソフト「エクセル統計」で有名なベルカーブ（社会情報サービス）のサイト「不偏分散の平方根は標準偏差の不偏推定量か」などを参考にしてほしい。

母分散の不偏推定量を「不偏分散」と言うならば，母標準偏差の不偏推定量は「不偏標準偏差」となるはずである。ところが，実際には，不偏分散の平方根を不偏標準偏差と呼ぶ人が結構いる。大学教員でさえ，しばしばそうであり，非常に奇妙に思ったので，ウィキペディア（Wikipedia）の標準偏差の項目に，私（Iguchi-Y）は，その例をいくつか書き加えておいた。兵庫大学・河野稔「健康統計の基礎・健康統計学 - 散布度」や神戸大学・中澤港「社会統計学（高崎経済大学非常勤講義）・第4回「記述統計(2)：代表値・分布のばらつき」が，それである。なお著者の現所属は異なる場合もある。

池田（2013）も，不偏分散の平方根を不偏標準偏差と書いている。しかも，「母標準偏差 σ を推定する値として得られるのが不偏標準偏差 u」（p.409 右段）と説明している。しかし，いくらなんでも，この説明は奇妙である。

池田（2013）が，「不偏標準偏差」を，単に「不偏分散の平方根」の意味で述べているのか，それとも，「母標準偏差の不偏推定量」だと誤解して述べているのか，はっきりしない。しかし，前者の意味ならば，母標準偏差の不偏推定量は何なのか，それをきちんと解説すべきであろう。この点，例えば，大村平「統計学のはなし」（日科技連，2014）では，不偏分散の平方根は，母標準偏差の不偏推定量ではない，と明確に記述している（同書，p.111）。それに関しては，私の別ページの解説を参照して欲しい。

水増し係数と割引き係数：不偏標準偏差と管理図係数

改めて，不偏標準偏差の定義を考えてみる。

母標準偏差の不偏推定量としての不偏標準偏差 U_s は，不偏分散 U² の平方根を，係数 c₄ で除した値となる。

\begin{align} U^2=\frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})^2 \end{align} \begin{align} c_4=\frac{\sqrt{\frac{2}{n-1}}\quad\Gamma\left(\frac{n}{2}\right)}{\Gamma\left (\frac{n-1}{2}\right)} \end{align} \begin{align} U_s=\frac{\sqrt{U^2}}{c_4} \end{align}

要するに，不偏分散の平方根を補正したのが不偏標準偏差なのである。この c₄ は，管理図（Control chart）係数として使われるものである。ただし，古典的手段として，管理図では係数表を使うことが多いので，実際には，c₄ の逆数を数値表に示し，それを不偏分散の平方根に乗じた値を不偏標準偏差として算出するのが一般的である。この c₄ の逆数が，大村（2014）が言う水増し係数に相当する。

3. シミュレーションによる不偏分散と不偏標準偏差

母平均 10，母分散 4 （つまり，母標準偏差 2）である正規分布と指数分布を想定し，大きさ 5 の標本（n = 5）として，統計ソフト R を用いて乱数を発生させて，不偏分散，不偏分散平方根，不偏標準偏差それぞれの平均値（不偏推定量）を計算し，それらを母分散および母標準偏差と比較してみた。

# 不偏分散，不偏分散平方根，不偏標準偏差の平均値（不偏推定量）

k<- 1000000  # 標本抽出回数
n<- 5
c4<- sqrt(2/(n-1))*gamma(n/2)/gamma((n-1)/2)
sigma<- 2
rate<- 1/sigma # 指数分布の母数

x<- replicate(k, {

  dat.norm<- rnorm(n, mean=10, sd=sigma)
  dat.exp<- rexp(n, rate=rate)

  c(
   var(dat.norm), sd(dat.norm),
   var(dat.exp), sd(dat.exp)
   )

})

# 不偏分散，不偏分散平方根，不偏標準偏差
#それぞれの平均
# 正規分布の場合
c(mean(x[1, ]), mean(x[2, ]), mean(x[2, ])/c4)
# 指数分布の場合
c(mean(x[3, ]), mean(x[4, ]), mean(x[4, ])/c4)

4. 結果と考察

シミュレーション結果の一例を表 1 に示す。

表1. 不偏分散，不偏分散平方根，不偏標準偏差それぞれの平均値
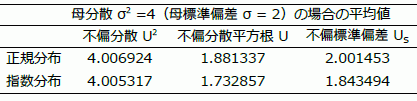
不偏分散と不偏標準偏差の平均値シミュレーション結果

正規分布の場合は，不偏分散 U² と不偏標準偏差 U_s が，文字通り，母分散 σ² と母標準偏差 σ の不偏推定量になると推定される。一方で，指数分布の場合は，U² は σ² の不偏推定量になると推定されるが，U_s は σ の不偏推定量にならないのである。すなわち，補正係数 c₄ は，どんな確率分布でも適用されるわけではないのである。

正規分布だろうが，指数分布だろうが，不偏分散平方根 U は母標準偏差 σ の不偏推定量にならないことは，一目瞭然である。池田（2013）は，果たして，このことを理解した上で，「母標準偏差 σ を推定する値として得られるのが不偏標準偏差 u」（p.409 右段）と述べているのか，はなはだ疑問である。大学教員であれば，そして，初学者向けの解説論文だからこそ，なおさら正確に説明すべきだが，そのような配慮に欠けていたと言わざるをえない。

なお，標準偏差を意味する英語 standard deviation を使い始めたのは，相関係数で有名なピアソン（Karl Pearson）である。

標準偏差の名付け親は，相関係数で有名なピアソン，不偏標準偏差の話題と共に

参考文献

池田郁男 (2013) 統計検定を理解せずに使っている人のために II．化学と生物 51(6): 408-417.

大村平 (2014) 統計学のはなし．日科技連．

ウェブサイトからの引用は，本文中の解説およびリンク先を参照。

Home