標準偏差の名付け親は,相関係数で有名なピアソン,不偏標準偏差の話題と共に
井口豊(生物科学研究所,長野県岡谷市)
最終更新:2022年1月1日
標準偏差の意味や計算法を知らなくても,その言葉自体は,耳にした人も多いと思う。少しでも統計学をかじった人なら,標準偏差を英語で Standard Deviation と書くことも知っているはずである。
ところがどうも,この Standard Deviation の由来,つまり,誰が名付けたかを知る人は,ずっと少ないらしい。そういえば,大学等で使われる統計学の教科書でも,この語の由来を記したものを私は知らない。
この語を最初に使ったのは,Karl Pearson である。日本人にとっては,相関係数で馴染み深い,あのピアソンである。それが公式に登場したのは,次の論文である。
Pearson, K. (1894)
Contributions to the Mathematical Theory of Evolution
Philosophical Transactions of the Royal Society of London. A, 71-110.
https://archive.org/details/philtrans02543681
この URL で全文を見られる。
そのページ右下の全画面記号(Toggle fullscreen)をクリックし,現れたページで右上のスピーカー記号(Read this book aloud)をクリックすると,論文を英語で読み上げてくれる。
この論文 5 ページ目(本文 p.75),下から 4 行目を見てほしい。
"standard-deviation" (Gauss's "Mean Error", Airy's "Error of Mean Square")
ガウスが Mean error (平均誤差)と呼び,エアリーが Error of Mean Square(平均平方誤差)と呼んだ計算式に対して,敢えて,ピアソンが standard-deviation と呼んだのである。
実は,これは公式な論文の話であって,非公式には, 1893 年 1 月 31 日の講義で,そう呼ばれていたようである。
このことは,数学用語の歴史的由来を解説した有名な次のサイトで知ることができる。ただし,日本人には案外知られていないサイトかもしれない。
Earliest Known Uses of Some of the Words of Mathematics
アルファベット順に用語が挙げられているので, S のページで, STANDARD DEVIATION を見ると
The term "standard deviation" was introduced in a lecture of 31 January 1893, as a convenient substitute for the cumbersome "root mean square error" and the older expressions "error of mean square" and "mean error."
ガウスの mean error などの用語は,専門的過ぎて分かりにくい(cumbersome),だからもっと簡単にして, standard deviation と呼ぶ,とピアソンは言ったのである。 もしかすると,自分の名付けた用語こそスタンダードだ,と言いたかったのかもしれない。実際,現在の状況を見れば,ピアソンの予想どおり(?),彼よりはるかに著名な科学者ガウスを差し置いて, standard deviation という呼称が,文字通り標準となっているのである。
なお,不偏標準偏差(Unbiased Standard Deviation),つまり,標準偏差の不偏推定量 D はは,標本サイズが大きくなると,近似的に,平均からの偏差平方和を n−1.5 で割った値の平方根として求められる。
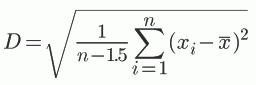
このことは次の論文に書かれている。
Brugger, R. M. (1969)
A note on unbiased estimation of the standard deviation.
The American Statistician, 23(4), 32-32.
不偏分散(Unbiased Variance) U2が,平均からの偏差平方和を n で割った形であることは良く知られている。
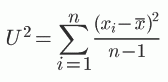
しかし, n−1 で割った不偏標準偏差の形は,あまり知られていないようである。ウィキペディア Wikipedia の標準偏差の項目にも書かれていなかったので,私 Iguchi-Y が書き加えておいた。
そこにも書いたことだが,困ったことに,不偏標準偏差の定義は二通りある。私が定義したように,標準偏差の不偏推定量 D を不偏推定量と呼ぶ人もいれば,不偏分散 U2 の平方根を不偏標準偏差と呼ぶ人もいるのである。どちらの定義が使われているか,十分注意が必要である。厳密に言えば,標準偏差の不偏推定量を不偏標準偏差と呼ぶべきだろう。これに関連して,次の統計解説ページも参照してほしい。
不偏標準偏差とは?:統計検定を理解せずに使っている人のために
不偏標準偏差については,管理図(Control chart)係数としても使われることもあり,次のページに解説した。
相関係数と Pearson の関わりで,余談になるが, Francis Galton (進化論で有名な Charles Darwin の従兄弟)が研究した回帰(Regrssion)という概念を,より数学的に洗練したのが Pearson である。以下の文献が参考になる。
Pearson, K. (1896)
VII. Mathematical contributions to the theory of evolution.
III. Regression, heredity, and panmixia
Philosophical Transactions of the Royal Society of London. Series A, containing papers of a mathematical or physical character (187): 253-318.
Gorroochurn, P. (2016)
On Galton's change from “reversion” to “regression”
The American Statistician 70(3): 227-231.
椎名乾平 (2016)
相関係数の起源と多様な解釈
心理学評論 59(4): 415-444.
相関係数を表す r は, Galton が唱えた「先祖返り(reversion)」に由来するとされ,この reversion が,その後の regression (回帰)に相当する。次の文献参照。
Rao, C. R. (1983)
多変量解析 その起源と発展に関する回想
応用統計学 12(2): 69-78 (柳井晴夫・竹内啓 訳).
「相関」と「回帰」の定義や用法の歴史的変遷についても,前述の Earliest Known Uses of Some of the Words of Mathematics を参照すると良い。
なお, Galton は,四分位数の概念も最初に唱えている。それに関しては,別ページ参照。