四分位数と四分位群：複数定義と用語の区別，その歴史

井口豊（生物科学研究所，長野県岡谷市）
最終更新：2024 年 10 月 17 日

1. はじめに

高校の段階でも学ぶようになった四分位数（Quartile）だが，これには複数の定義があり，高校の教育界で物議を醸したことがある。 四分位数の定義（計算の仕方）が，高校授業で学ぶものと， Excel で算出されるもので異なるのである（参照：四分位数の定義）。

教科書出版会社「数研」の 数研通信 78号 2014年1月 教科書の内容に関するQ＆Aにある「四分位数の定義」も参照してほしい。この Q&A の中で，高校数学で の四分位数の定義 を決めた文部科学省の説明が，「一番簡単な定義である」というのが興味深い。

2. 高校数学での四分位数の定義とその他の定義

高校数学で示された四分位数の定義に基づいて，例えば，以下のような奇数個，偶数個データ 2 例の四分位数を求める。

具体的な計算については，教科書を見て，各自やってみて欲しい。結果だけ述べると，以下のようになる

しかし実際には，最初に述べたように，これ以外の定義（計算法）による四分位数もありうる。ここでは，統計解析ソフト R の quantile 関数を使って，前述のデータに対して， 9 種類の 四分位数を算出してみよう。

まず自作の qt 関数を作り，表形式で，これらの 四分位数を表示させる。

さらに，位置の代表値（measure of location）として，中央値だけでなく，中央ヒンジ（mid-hinge）も計算出力させる。中央ヒンジに関しては，別ページ参照（四分位偏差は，どのように使われるか？変動係数の話題も含めて）。

## 9 種類の四分位数を計算・表示する関数 ##
qt<- function(x) {
  table<- matrix(as.numeric(NULL), 9, 3)

  for (type in 1:9) {
  table[type, ]<- quantile(x, c(1/4, 1/2, 3/4), type=type)
  }

  mh<- (table[, 1] + table[, 3])/2
  Type<- 1:9

  table<- cbind(Type, table, mh)

  dimnames(table) <- list(1:9, c("Type", "Q1", "Q2", "Q3", "Midhinge"))
  return(round(table, 3))
}

## データ ##
a<- c(1, 5, 7, 10, 13, 16, 18, 20, 24)
b<- c(1, 5, 7, 10, 14, 18, 20, 24)

##  9 種類の四分位数，中央値，中央ヒンジ ##
qt(a)
qt(b)

結果は以下の通り。

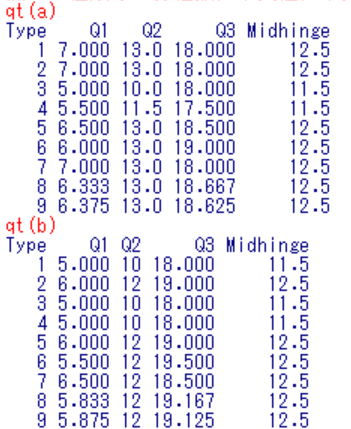
この結果から，前述の高校数学での四分位数が，以下のタイプで計算されたことが分かる。

高校では，わざわざ，奇数偶数で異なる定義の計算を行い，しかも，この方法は汎用性があるとは言えない。すなわち，まず中央値（メディアン，median，第 2 四分位数に相当）を決め，その上下に，第 1，第 3 四分位数を決めている。これでは，例えば，この定義で五分位数（quintile）を計算しろと言われても困惑してしまうだろう。なお，四分位数に複数定義が存在するのだから，当然だが，中央値も定義によって異なる。それは上記の結果から明らかである。

3. Excel による四分位数の定義

Excel 2019 による四分位数を QUARTILE.EXC, QUARTILE.INC, QUARTILE の各関数で求めた結果が以下のとおりである。 Excel でも，関数によって定義が異なることがわかる。ただし，奇数個・偶数個のような場合分けは無い。

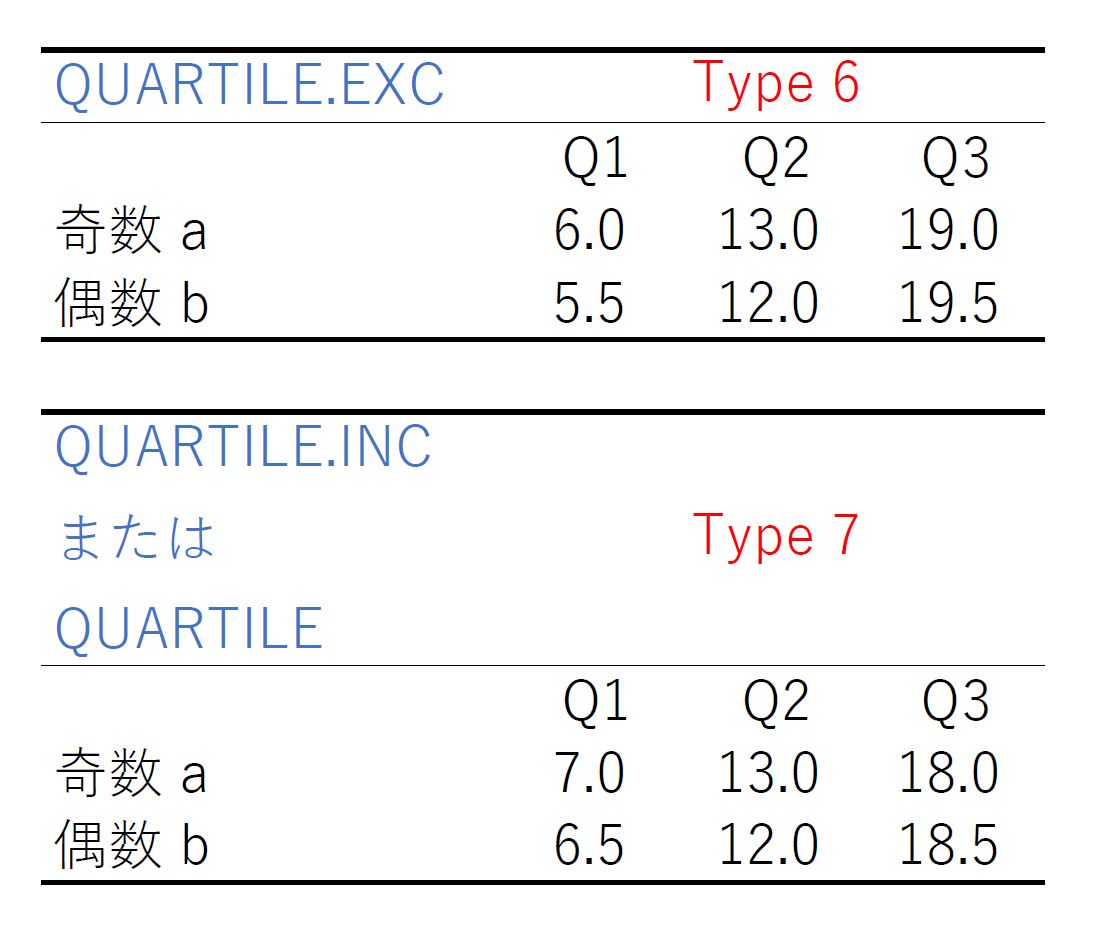
今や中高生でもパソコンを扱う時代である。彼らが将来，統計データを解析するときもパソコンや統計ソフトが頼りとなるであろう。それを見越して，高校生の時から，統計ソフトで 四分位数がどのように計算されているか，それを解説するような授業をしてほしい。

四分位数が定義によって異なれば，当然ながら，それを利用した箱ひげ図も異なったものになる。それにも注意が必要だが，ほとんど触れられていない現状がある。

• 箱ひげ図は四分位数の定義で異なる: geom_boxplot と boxplot
• 箱ひげ図 skeletal と schematic，外れ値と 3 シグマ

4. 四分位数によって分けられたデータの名称

ここまで述べてきた四分位数は，順序化されたデータを 4 等分する区切りの値（value）である。一方で，そのようにして 4 等分されたデータの集団（group）に対しては，文字通り， 四分位群（Quartile group） と呼ばれる。個々の集団は，日本語では，第 1，第 2，第 3，第 4 四分位群と呼ばれる。例えば，以下の論文がその例である。

深谷幸生・大野良之・松本忠雄・荒深美和子（1987）
血中鉛量と血圧：某二事業所での鉛検診資料から
日本衛生学雑誌, 42(3): 754-761.

それらは英語でも，それぞれ文字通り， the first, second, third, fourth group と呼ばれ，以下の論文にその例が見られる。

Foo, K. et al. (2003)
A single serum glucose measurement predicts adverse outcomes across the whole range of acute coronary syndromes
Heart, 89: 512-516.

この論文では，冒頭の Abstract にも以下のように書かれていて，理解しやすい。

The patients were stratified into quartile groups (Q1 to Q4).

英語の場合，注意すべき点は， quartile 自体に， 四分位数と 四分位群の意味が存在することである。例えば，英語辞書 Oxford Dictionary of English (ODE, third ed.) で quartile の最初の定義を見ると，次のように書かれている。

each of four equal groups into which a population can be divided according to the distribution of values of a particular variable.

これが，4つに分けられたグループ，つまり「 四分位群」を意味することが分かる。

二番目の定義として， いわゆる「四分位数」が載っている。

each of the three values of the random variable which divide a population into quartiles.

学術論文で quartile が四分位群の意味で使われている例としては，次のものを参照。

Kamycheva, E., Joakimsen, R. M., & Jorde, R. (2003)
Intakes of calcium and vitamin D predict body mass index in the population of Northern Norway
The Journal of nutrition 133(1): 102-106.

その p.103 を見ると，次のような説明となっている。

Vitamin D intake in both genders was divided into 4 quartiles

つまり， quartiles で quartile groups を表している。

前述の ODE にも載っているように， quartile の語源はラテン語の「四分の一」なので， 四分位数よりも， 四分位群の定義のほうが，一般の人にとっては自然かもしれない。実際，英語のテレビや新聞などでは， quartile を四分位群の意味で使うほうが多く見られる。私自身も，学生時代， 最初に知った quartile の用例は，四分位群という意味だった記憶がある。

かつて NHK ラジオ第 2 で放送された「実践ビジネス英語」（2018年1月13日放送）では， quartile が，統計学の教科書で一般的に使われる 「四分位数」の意味ではなく，「 四分位群」の意味で解説されていた。もちろん，どちらも正しい用法であるが，文脈によって区別が必要である（NHK実践ビジネス英語：統計学用語・四分位quartileを巡って）。

四分位数に限らず，一般に分位数を表す英語である「クォンタイル (quantile)」には，等分割する値（value）の意味と，そのようにして分割された群（group）の二つの意味がある。英語文献を読んだり，ニュースを聞いたりする際は，その点に注意が必要である。ウィキペディアの分位数にも，そのような解説が無かったので，私が追記した（2016年10月24日 (月) 13:37; Iguchi-Y）。

そのようにして等分割された群に対して，総務省統計局は，分位階級という用語を用いている。英語で，そのような用語が使われている論文は，以下のもの参照。

Yemiru, T. et al. (2010)
Forest incomes and poverty alleviation under participatory forest management in the Bale Highlands, Southern Ethiopia
International Forestry Review, 12(1): 66-77.

この論文の例えば， Table 4 に， Income Quintile class と書かれている。

分位数 quantile の用語としての歴史を知るには，以下の論文が役立つ。

Aronson, J. K. (2001)
Francis Galton and the invention of terms for quantiles
Journal of clinical epidemiology, 54: 1191-1194.

この論文の最初のページ第 2 段落で，まず quantile の定義に触れられている。そこでは，英語辞書 Oxford English Dictionary (OED) の定義が引用されている。

each of any set of values of a variate which divide a frequency distribution into equal groups, --- also, any one of the groups so produced

ここでも， quantile に数（value）と群（group）の意味があると分かる。

それに続いて quantile という単語の歴史が論じられる。これが the late 19th century に現われたということなので，意外と新しい用語なのである。さらに，ある数値の範囲を等分してグループ分けするというアイデアは， Francis Galton によるものなのである。彼は，進化論で有名な Charles Darwin の従兄弟にあたる。ただし OED が， quartile という単語を最初に用いたのは Donald McAlister であるとしていることも，以下の論文とともに紹介されている。

McAlister, D. (1879)
XIII. The law of the geometric mean
Proceedings of the Royal Society of London, 29(196-199), 367-376.
DOI: 10.1098/rspl.1879.0061

大学の授業でも，統計量としての 四分位数の定義や計算式だけでなく，上記のような語法やその歴史に，簡単で良いので触れてほしいものである。

quartile に限ったことではないが，数字が絡むと，英単語や英熟語（もちろん，その他の外国語でも）の微妙な意味の違いが，大きな問題を招くことがある。以下の論文は，太田邦昌の「more than 誤訳論争」に対して，科学教育の観点も含めて，私が意見を述べたものである。大学受験用の英語問題集にさえ，数値関連の誤訳が見られることも指摘した。

井口豊（1994）
なぜ"more than"を誤訳するのか？
生物科学，46(3): 159-163.