logo
生物科学研究所 井口研究室
Laboratory of Biology, Okaya, Nagano, Japan
Home

箱ひげ図 skeletal と schematic，外れ値と 3 シグマ

井口豊（生物科学研究所，長野県岡谷市）
最終更新： 2022 年 11 月 1 日

1. はじめに

箱ひげ図には，大きく分けて 2 種類あり，一つは，データ全体の範囲を表現するもの，もう一つは，データの一部の範囲を表現し，外れ値を付記するものである。

前者は skeletal boxplot，後者は schematic boxplot と呼ばれ，それぞれ Velleman and Hoaglin (1981)，Tukey (1977) が最初に命名したようだ。それぞれの文献の p.66 と p.48 に，その名称が登場する。

このうち，skeletal boxplot は 5 数要約（5-number summary）を視覚化したものであり，その表現法自体は Tukey (1977) にも見られるが，彼は schematic boxplot を推奨している（p.41）。

2. ヒゲの作り方

どちらの箱ひげ図も，縦方向に表現した場合，箱の高さが四分位範囲（interquartile range, IQR）を示す。その上で schematic boxplot のヒゲの長さは，下ヒゲで，箱の高さの 1.5 倍を第 1 四分位数から減じ，また，上ヒゲで，箱の高さの 1.5 倍を第 3 四分位数に加えて作成される。これが， Tukey (1977) が示した一つの基準（a useful rule of thumb, p.44）であり，現在でも様々な統計ソフトで標準的に使われる（参考文献は，最後に一括した）。例えば， SPSS 例: 箱ひげ図や jmp 外れ値の箱ひげ図の説明が，それである。

すなわち，式で表すと，以下のようになる。

下ヒゲ下端 = Q1 − 1.5 IQR
上ヒゲ上端 = Q3 + 1.5 IQR

ただし，正確に言えば， R では，この範囲内の最大または最小となるデータ点までをヒゲの長さとしている。例えば，パッケージ ggplot2 の geom_boxplot, Summary statistics には以下のような説明がある。

The upper whisker extends from the hinge to the largest value no further than 1.5 * IQR from the hinge (where IQR is the inter-quartile range, or distance between the first and third quartiles).

基本グラフ関数の boxplot, range にも同様な説明がある。単純に， 1.5 IQR の長さではないことに注意しよう。

3. ヒゲの長さが持つ意味

標準正規分布を仮定し，ヒゲの長さが持つ意味を考えてみよう。例えば，統計ソフト R で計算すると以下のようになる。 


####
# 上ヒゲ上端の正規分布パーセント点
IQR<- qnorm(0.75) - qnorm(0.25)
uw<- qnorm(0.75) + IQR * 1.5 
uw

# 下ヒゲ下端の正規分布パーセント点
IQR<- qnorm(0.75) - qnorm(0.25)
lw<- qnorm(0.25) - IQR * 1.5 
lw

# 下ヒゲ下端と上ヒゲ上端の間の正規分布確率
p<- pnorm(uw)- pnorm(lw)
p
######

結果は以下のようになる。

上ヒゲ上端の正規分布パーセント点
2.697959

下ヒゲ下端の正規分布パーセント点
-2.697959

下ヒゲ下端と上ヒゲ上端の間の正規分布確率
0.9930234

要するに，管理図にしばしば使われる 3 シグマ基準に近い外れ値の境界値であり，その内側は約 99% のデータが含まれる範囲なのである。

4. schematic boxplot による外れ値認定の注意点

前述のように， schematic boxplot が，外れ値の簡便な検出法のように使えるのだが，逆に言えば，ヒゲの外側を何でもかんでも外れ値と判断してしまう危険性も持っている。

極端な例だが， R ggplot2 を使い，大きさ 10000 の正規乱数で， schematic 箱ひげ図を作成してみた。 


######
library(ggplot2)

# 標準正規乱数，大きさ 10000
set.seed(10)
x<- rnorm(10000)

df<- data.frame(x)

# schematic boxplot
sb<- ggplot(df, aes(x = "", y = x)) +
    stat_boxplot(geom = "errorbar", width = 0.2) +
    geom_boxplot(
      col = "black", fill = "lightgray",
      outlier.colour = "red",
      outlier.fill = "red"
    ) +
    theme_classic()

sb
###############

結果は以下の図 1 のようになった。

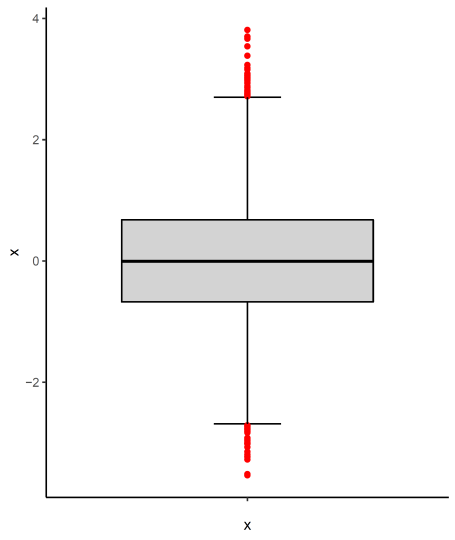
正規乱数に対する schematic 箱ひげ図

図 1. 正規乱数（n = 10000）に対する schematic 箱ひげ図

データ分布の両側に，外れ値だらけ，といった感がある。そこで，このデータ分布をヒストグラムで表現してみる。 


######
# ヒストグラム
wh<- as.numeric(
   ggplot_build(sb)$data[[1]][1:5]
    )

df$outlier<- df$x > wh[5] | df$x < wh[1]

bd<- data.frame(
   bdx = c(wh[1], wh[5]),
   boundary = c("red", "red")
)


h<- ggplot(df, aes(x, fill = outlier)) +
   geom_histogram(
     breaks = seq(-4.2, 4.2, by = 0.3)
     ) +
     geom_vline(data = bd,
        aes(
         xintercept = bdx,
         color = boundary
       ))+
   theme_classic() +
   scale_fill_manual(values=c("lightblue", "red"))

h

###############

結果は以下の図 2 のようになった。

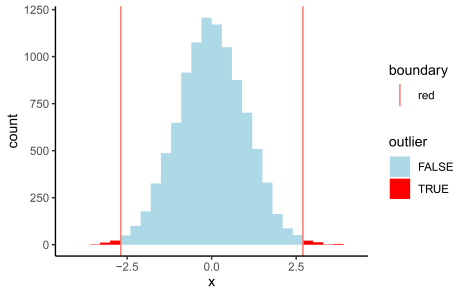
正規乱数に対するヒストグラム

図 2. 正規乱数（n = 10000）に対するヒストグラム

もし schematic 箱ひげ図で，ヒゲの外側のデータを外れ値として除去してしまうと，せっかく正規分布に従うデータが得られたのに，両端が切り落とされた分布（truncated distribution）になってしまうのである。これは schematic 箱ひげ図だけの問題ではなく， 3 シグマ基準で外れ値とする場合も同様に生ずる問題である。

このように， schematic 箱ひげ図で外れ値を認定するときには，十分注意が必要である。このことに関しては， Dawson (2011) が参考になる。

参考文献

Dawson, R (2011) How significant is a boxplot outlier?. Journal of Statistics Education 19 (2): 1-12.

Tukey, J. W. (1977) Exploratory Data Analysis, Addison-Wesley.

関連サイト

Home