logo
生物科学研究所 井口研究室
Laboratory of Biology, Okaya, Nagano, Japan
Home

水増し係数と割引き係数：不偏標準偏差と管理図係数

井口豊（生物科学研究所，長野県岡谷市）
最終更新：2024 年 4 月 21 日

1. はじめに

統計学のはなし（大村 平 著，日科技連，2014）の中で，母標準偏差の不偏推定量を求めるのに，「水増し係数」と「割引き係数」という 2 種類の係数表が掲載されている。ところが，この計算式の解説が無い。ここでは，それらの係数と管理図（Control chart）係数の関連を示しながら，実際の計算を行なってみる。

なお，不偏分散の平方根，いわゆる n−1 で割る分散の平方根は，不偏標準偏差ではないので，注意すべきである。それに関しては，次のページを参照してほしい。

不偏標準偏差とは？：統計検定を理解せずに使っている人のために?

2. 水増し係数

まず，水増し係数には，管理図における係数 c4 が使われていることを理解しておく必要がある。大村も，「水増し係数」などと書かずに， c4 を用いた記述をすべきだった。大村は， p.112 で，水増し係数が，「統計の専門書には 1/c4 という記号で書いてあり」と述べているが，私としては，Xbar-s 管理図で使われる c4 を使って計算したのが「水増し係数」という印象が強い。

c4 の定義式はガンマ関数を使って次のようになる。

\begin{eqnarray} c_4=\frac{\sqrt{\frac{2}{n-1}}\quad\Gamma\left(\frac{n}{2}\right)}{\Gamma\left (\frac{n-1}{2}\right)} \end{eqnarray}

この c4 の逆数 1/c4 は，正規母集団の標準偏差を不偏推定する係数として使われる。すなわち，不偏分散の平方根（いわゆる， n−1 で割る標準偏差）に 1/c4 を乗ずると不偏標準偏差となる。したがって，水増し係数を c とすると次のように表される。

\begin{eqnarray} c=\sqrt{\frac{n}{n-1}}\quad\frac{1}{c_4} \end{eqnarray}

標本の標準偏差（いわゆる， n で割る標準偏差）を使う水増し係数では， n/(n−1) の平方根を乗じた式になる。

最初に述べた c4 の定義式を代入すると，水増し係数 c は次のようになる。

\begin{eqnarray} c=\frac{\sqrt{\frac{n}{2}}\quad\Gamma\left(\frac{n-1}{2}\right)}{\Gamma\left (\frac{n}{2}\right)} \end{eqnarray}

統計解析ソフト R で実際に「水増し係数」を計算してみよう。 

# 水増し係数 c を求める

n<- c(
  2:10, 12, 14, 16, 20, 30, 40, 50
)

c<- as.numeric(NULL)

for (i in 1:length(n)) {

 c[i]<- sqrt(n[i]/2)*gamma((n[i]-1)/2)/gamma(n[i]/2)

}

# 水増し係数表
data.frame(n, c=round(c, digits=2))
# 終了

結果は，次のようになる。

表 1. 水増し係数表

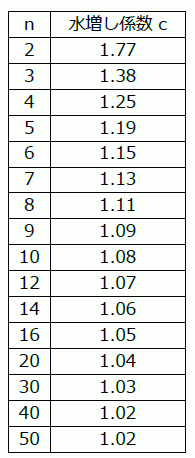
水増し係数表

「統計学のはなし」（2014）の p.112 の水増し係数表では，
n = 9 のとき, c = 1.10
n = 50 のとき, c = 1.01
となっていて，小数第 2 位で数字が異なる。

念のため，数値計算ソフト Maxima で，この部分を計算してみると，以下のようになる。 

f(n):=sqrt(n/2)*gamma((n-1)/2)/gamma(n/2)$
float(f(9));
float(f(50));

結果は，それぞれ
1.094241683386788
1.015319194596484
となって，小数第3位で四捨五入すると， R と同じ結果となった。

3. 割引き係数

割引き係数には，管理図における係数 d2 が使われている。これもまた，大村は「割引き係数」と呼ばずに， d2 を使って説明すべきだった。 d2 は，Xbar-R 管理図 で使われる。この場合の R は，もちろん，Range（範囲） を意味する。

係数 d2 は，水増し係数で使われた c4 に比べると面倒な計算で，標準正規分布の累積分布関数を Φ(x) とすると，次のような積分値で表される。

\begin{eqnarray} d_2=\int_{-\infty}^{\infty}\left[1-(1-\Phi(x))^n-(\Phi(x))^n\right]dx \end{eqnarray}

割引き係数を d とすると，それは d2 の逆数として表される。

\begin{eqnarray} d=\frac{1}{d_2} \end{eqnarray}

統計解析ソフト R で実際に「割引き係数」を計算してみよう。 

# 割引き係数 d を求める

n<- 2:10

d<- as.numeric(NULL)

for (i in 1:length(n)) {

fd<- function(x){
  1-(1-pnorm(x))^n[i]-pnorm(x)^n[i]
}

d[i]<- 1/integrate(fd, -Inf, +Inf, rel.tol=1e-8)$value

}

# 割引き係数表
data.frame(n, d=round(d, digits=3))
# 終了

結果は，次のようになる。

表 2. 割引き係数表

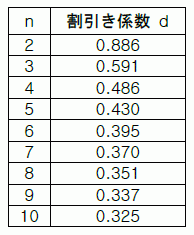
割引き係数表

「統計学のはなし」の p.113 の割引き係数表と同じ数値になった。

関連ページ

シューハート管理図係数の計算

Home