logo
生物科学研究所 井口研究室
Laboratory of Biology, Okaya, Nagano, Japan
Home

シューハート管理図係数の計算

井口豊（生物科学研究所，長野県岡谷市）
最終更新：2022年8月22日

1. はじめに

品質管理（QC, Quality Control）の問題で必須のシューハート管理図係数（Shewhart control chart constant）だが，ほとんどのサイトの説明では，「係数表を引け」となっている。パソコンが容易に使える時代なのに，相変わらず陳腐な説明が多く，気になっていた。ソフトを利用すれば，係数を算出してくれるものあるようだが，ここでは，統計ソフト R を用いて，定義式となる積分を数値計算して，とりあえず A2, D3, D4 係数を求めてみる。なお，日本語では，これらは係数と呼ばれるが，英語の直訳すれば，むしろ「定数（constant）」と呼ぶべきである。

2. 管理図係数の定義式

まず，基本となる係数 d2， d3 を標準正規分布の累積分布関数 Φ(x) を用いて定義する。

\[ d_2=\int_{-\infty}^{\infty}\left[1-(1-\Phi(x))^{n}-(\Phi(x))^{n}\right]dx \] \[ d_3=\sqrt{2\int_{-\infty}^{\infty}\int_{-\infty}^{y}\left[1-(\Phi(y))^{n}-(1-\Phi(x))^{n}+(\Phi(y)-\Phi(x))^{n}\right]dxdy-d_2^2} \]

A2，D3，D4 は，以下のように定義される。

\[ A_2=\frac{3}{\sqrt{n}d_2} \] \[ D_3=1-3\frac{d_3}{d_2} \] \[ D_4=1+3\frac{d_3}{d_2} \]

3. 管理図係数の計算

統計解析ソフト R で A2，D3，D4 を n = 50 まで，小数点以下 4 桁で計算してみよう。もちろん，パソコンの性能と時間が許す限り，任意の n まで計算できるし，桁数もさらに多くできる。 


### 管理図係数の計算 ###
d2<- as.numeric(NULL)
d3<- as.numeric(NULL)
A2<- as.numeric(NULL)
D3<- as.numeric(NULL)
D4<- as.numeric(NULL)

n<- 1:50

for (i in n[n>=2]) {

# d2の計算
  fd2<- function(x){
    1-(1-pnorm(x))^i-pnorm(x)^i
  }

d2[i]<- integrate(fd2, -Inf, +Inf, rel.tol=1e-8)$value

# d3の計算
  fd3<- function(y){

     f<- function(x){
      1-pnorm(y)^i-(1-pnorm(x))^i+(pnorm(y)-pnorm(x))^i
      }

  integrate(f, -Inf, y, rel.tol=1e-8)$value
  }

d3[i]<- sqrt(2*integrate(Vectorize(fd3), -Inf, +Inf, rel.tol=1e-8)$value-d2[i]^2)
}

# A2, D3, D4 の計算
A2<- 3/(sqrt(n)*d2)
D3<- 1-3*d3/d2
D4<- 1+3*d3/d2

# 係数表
subset(round(
 data.frame(n=n, A2=A2, D3=D3, D4=D4), 
digits=4), n>=2)
###########

結果は，次のようになる。

表 1. シューハート管理図係数表（PDF）

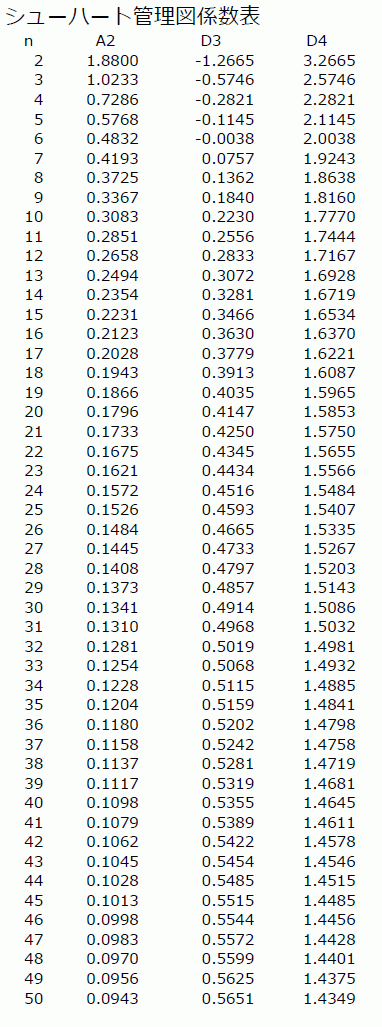
シューハート管理図係数表

n が 25 程度までなら，ネット上にも表があるので，それと比較してみてほしい。例えば， Shewhart Constants for Control Charts を見ると，私の結果と一致している。

この表で面白いのは， D3 で n が 6 以下の場合，係数が負になる点である。たいていの表では，この部分を空白にしたり， 0 としている。さらに，その解説も，「計算できない」などと，漠然とした説明になっている場合が多いが，定義に従って計算すると，その部分の係数は負になるのである。

関連ページ

水増し係数と割引き係数：不偏標準偏差と管理図係数

Dixon の Q 検定（外れ値検定）を R で計算：統計表の作成

Home