決定係数は回帰のバラツキ指標ではない

井口豊（生物科学研究所，長野県岡谷市）
最終更新：2021年1月22日

決定係数が何を表すのか，そして，その計算式が何を意味するのか，どうも理解していない人が多いようだ。特に，原点通過の回帰直線の決定係数の問題点は，以下のページ参照：
決定係数R2の誤解：必ずしも相関の２乗という意味でなく，負にもなるし，非線形回帰には使えない

「決定係数は，回帰式の適合度の指標であり，その数値が大きい（1 に近い）ほど，当てはまりが良いことを示す」，と説明される。しかし，決定係数は，データの y 方向の全変動を基準とした時の回帰変動の相対的数値を表している。回帰式からのデータのバラツキ程度を表すものではなく，むしろ，抽象的な概念と言えよう。

困ったことに，全変動の定義が複数あることが，決定係数の定義の違いの原因ともなっている。その点は，以下の解説ページを参照：
決定係数 R2 の違い: Excel, OpenOffice, LibreOffice および統計解析ソフト R を用いて

例えば，統計解析ソフト R を用いて，次のような2群 A と B の二次元 (x, y) データを回帰分析してみよう。

# A群データ
x1<- c(0.7, 3.3, 8.5, 8.7)
y1<- c(0.7, 5.2, 3.7, 9.1)

# B群データ
x2<- c(8.4, 3.9, 8.0, 2.1)
y2<- c(1.6, 1.6, 4.8, 3.7)

なお，これらのデータのサンプル数（標本数）は 2 であり，サンプルサイズ（標本の大きさ）は各 4 である。2 群（2 標本）それぞれに4対のデータを含んでいる。サンプル数とサンプルサイズを混同しないでほしい。

これらのデータに，回帰直線（regression line）を当てはめ，グラフ化してみる。

res1<- lm(y1~x1)
res2<- lm(y2~x2)

par(mfrow=c(1, 2))

plot(x1, y1,
xlim=c(0, 10), ylim=c(0, 10),
main="Group A")
abline(res1)

plot(x2, y2,
 xlim=c(0, 10), ylim=c(0, 10),
main="Group B")
abline(res2)

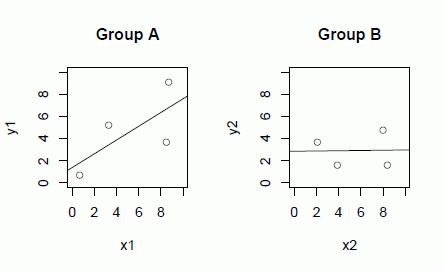
比較しやすいように，両軸のスケールを両群で同じにしてある。求められた回帰直線は，次のようになった。

A: y = 0.62x + 1.38
B: y = 0.011x + 2.86

直感的に，どちらの群において，回帰直線からのデータのバラツキが小さいと感じるだろうか？あるいは，どちらの群の直線の適合度が高いと感じるだろうか？私には，視覚的な判断は難しいと感じるが，あなたならどう思うだろうか？

回帰分析の結果全体を一挙に見たければ，以下のようにすれば良い。

summary(res1)
summary(res2)

回帰直線からのデータのバラツキは，残差平方和（残差の２乗和，Residual sum of squares）を自由度 n−2 で割った残差分散（residual variance）で表される。さらに，これの平方根は残差標準偏差（residual standard deviation）と呼ばれる。

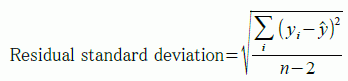
R では残差標準誤差（residual standard error）と記されるが，これは誤記かもしれない。

R の help で， summary() が返す sigma の内容についてみると
Extract Residual Standard Deviation 'Sigma'

その Note に以下のように書かれている。

The misnomer "Residual standard error" has been part of too many R (and S) outputs....

自由度の計算で，標本サイズ n から2を引いたのは，直線の傾きと y 切片を推定したためである。

残差分散や残差標準偏差は，一般的な記述統計量として用いられる不偏分散やその平方根と考え方は基本的に同じである。不偏分散は，平均からの偏差平方和をなぜ n−1 で割るのか，と時々質問されるが，それに関しては，以下のページ参照。

標本分散と標本不偏分散，n で割るか n-1 で割るか，不偏標準偏差の話題も含めて

R において，回帰分析の結果から残差標準偏差だけ取り出すには，文字通り， sigma とすれば良い。

summary(res1)$sigma
summary(res2)$sigma

その結果
A: σ = 3.041421
B: σ = 1.952397
となり， B のほうが回帰直線からのデータのバラツキが断然小さいのである。残差の箱ひげ図（box plot）を作成すると，視覚的に理解しやすい。

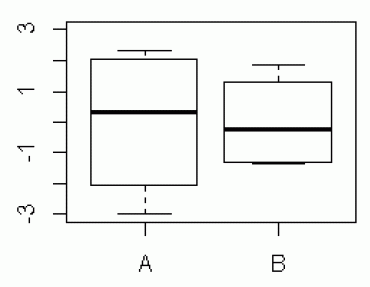
最初の図のような，回帰直線とデータの x-y プロット（scatter plots）を見ただけでは，このようなデータのバラツキの違いは分かりにくい。

一方で，決定係数 R2 だけを回帰分析の結果から取り出すには， r.squared を付ければ良い。

summary(res1)$r.squared
summary(res2)$r.squared

その結果
A: R2 = 0.4946259
B: R2 = 0.000496774

すなわち，回帰直線からのデータのバラツキが大きい A のほうが，決定係数が大きいのである。 B の決定係数は，ほぼ 0 であり，決定係数が回帰の適合度の指標と言うなら， B の回帰直線は適合度ほぼゼロということになる。

以上の結果をまとめると
A：回帰からのバラツキ大，決定係数大・・適合度が良い？
B：回帰からのバラツキ小，決定係数小・・適合度が悪い？
となる。

再度述べるが，このようなことが起きるのは，決定係数がデータの全変動を考慮に入れて，それに対する回帰変動の割合を計算しているためである。 B のように，回帰の傾き（0.011）が小さくなると，全変動に対する回帰変動の割合が小さくなるので，決定係数も小さくなるのである。案外，そのことを念頭に置かず，単に，決定係数が大きければ適合度が高い，というような安易な解説をおこなっている人もいる。

逆に言えば，このページのタイトルどおり，決定係数は回帰直線からのデータのバラツキ程度を表すものではない，ということである。この意味で， 決定係数が直感的に見ても使い勝手の良いものとは言えず，むしろ使用を避けるべきものとさえ言えよう。

今回の分析のように，大きさが等しいとは言え，異なる 2 標本で決定係数を安易に比較できない，という問題はある。しかし，逆に言えば，冒頭のような個々の回帰直線のグラフと決定係数のみを見て，グラフの当てはまりが良いとか悪いとか単純に判断してはいけない，ということでもある。