Excelグラフ累乗，指数，多項式近似の論文記載の注意

井口豊（生物科学研究所，長野県岡谷市）
最終更新：2024 年 4 月 27 日

1. はじめに

Excel のグラフや関数を用いて，累乗近似や指数近似を行なう場合，それは，データを対数変換した上で，直線回帰として最小二乗法を適用している。したがって，その結果を論文やレポートに記す場合は，「データを対数変換して直線近似した」と書かないと正しいとは言えない。ここでは，例を挙げて，実際にデータ解析して説明する。

なお，本ウエブサイトは，以下の論文で引用されている。

秀島好知・岩城雄飛・山口栞・河野太祐 (2021)
佐賀県水稲作況試験における NDVI (正規化植生指数) と生育診断指標との関係
日本作物学会九州支部会報 87: 6-12.

2. データ解析例

次のデータを用いて累乗近似を行う。

x: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
y: 6, 12, 27, 50, 75, 108, 149, 198, 249, 303

求めるのは，次の式の母数（パラメータ） a, b である。

\begin{align} y=ax^b \end{align}

なお，母数の意味も誤解されやすいので，以下のページで確認：
統計学の基本用語．母数は分母でも全数でもない！：母数とは母平均や母分散

統計解析ソフト R による，データの対数変換・線形回帰による結果と，非線形回帰による結果を比較してみる。


# R スクリプト
#　近似データ
x<- c(1: 10)
y<- c(6, 12, 27, 50, 75, 108, 149, 198, 249, 303)

# データを対数変換した後，線形回帰
# 対数変換
ln.x<- log(x)
ln.y<- log(y)

# 線形回帰
line<- lm(ln.y~ln.x)

# パラメータ a
(as<- exp(line$coef[1]))

# パラメータ b
(bs<- line$coef[2])

# 残差平方和
sum((y-as*x^bs)^2)

# 散布図と Excel 累乗近似（Rで描画した場合）
plot(x, y, xlim=c(0, 11),
　 main="対数変換・線形回帰の累乗近似")
curve(as*x^bs, add=T, col="red")
# 終了

対数変換・線形回帰の結果
a: 4.45247
b: 1.792387
残差平方和: 1401.634

これが，Excel グラフのよる累乗近似である。

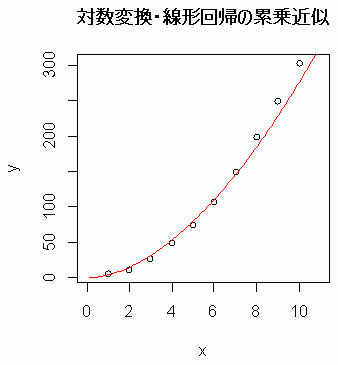
Excel 対数変換・線形回帰の累乗近似

図1. Excel 対数変換・線形回帰の累乗近似．

これをよく見て欲しいのだが，右端に近づくと，データと近似曲線のズレが大きくなるのが分かる。対数変換すると，大きな値のズレを過小評価してしまうために，このようなことが起きる。

次に，非線形回帰で累乗近似してみる。


# R スクリプト
# 非線形回帰
nonline<- nls(y~at*x^bt, start=c(at=1, bt=1))

# パラメータ a
(at<- coef(nonline)[1])

# パラメータ b
(bt<- coef(nonline)[2])

# 残差平方和
sum((y-at*x^bt)^2)

# 散布図と Excel 累乗近似（Rで描画した場合）
plot(x, y, xlim=c(0, 11), main="非線形回帰の累乗近似")
curve(at*x^bt, add=T, col="red")
# 終了

非線形回帰の結果
a: 3.065695
b: 1.997829
残差平方和: 30.93659

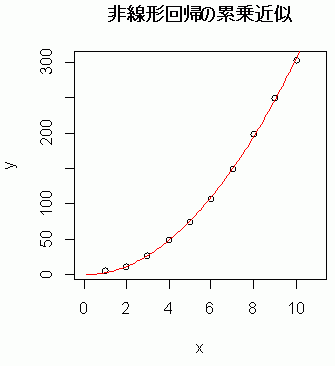
非線形回帰の累乗近似

図2. 非線形回帰の累乗近似．

前述の対数変換・線形回帰の結果と比べると，パラメータがかなり異なることが分かる。また，非線形回帰のグラフのほうが，ほぼピタリとデータと累乗曲線が一致することが分かる。当然ながら，非線形回帰のほうが残差平方和も小さい。

つまり，単純に，データ点に近い曲線を求めたいならば，非線形回帰を行なう必要があるのだ。指数曲線近似の場合も同様であり，以下のサイトの例は，非線形問題であることは全く考慮されていない：
高級泡盛の秘密に迫る　(価格決定式編)

さらに，このサイトでは，非線形回帰に対して使ってはいけない決定係数を用いて指数曲線の適合度を評価している。この点も，私の別ページの解説を参照：
決定係数R2の誤解：必ずしも相関の２乗という意味でなく，負にもなるし，非線形回帰には使えない

この点， R では線形回帰と非線形回帰で表示法を区別している。


# 線形回帰の詳細
summary(line)

# 決定係数が計算，表示される
Multiple R-squared: 0.9867

# 非線形回帰の詳細
summary(nonline)
# 決定係数が計算されない

実は，Excel の場合，累乗近似曲線の R² を求めているのではなく，対数変換データの近似直線の R² を求めているのである。その点も別ページの解説を参照：
Excel両対数グラフで近似直線が曲線になる理由

なお注意したいのは，対数変換・線形回帰と非線形回帰のどちらが絶対正しいかという問題ではない，という点である。例えば，対数変換したほうが残差が正規分布に近づくのであれば，対数変換・線形回帰のほうが理論的には妥当かもしれない。

いずれにしろ，自分のやっている近似あるいは回帰が，どのような理論的計算に基づいているのか，それに注意すべきであり，それを論文やレポートに記すべきなのである。

回帰式による直線や曲線からのデータのバラツキの指標としては，残差分散（residual variance）がある。時として誤解されがちだが，決定係数 R² は，そういう意味の指標ではない。それに関しては，次のページ参照：
決定係数R2は回帰のバラツキ指標ではない

3. まとめ

Excel グラフで近似曲線を求める方法の注意点を理論的にまとめてみる。

Excelグラフで求められる累乗近似式

\begin{align} y=ax^b \end{align}

あるいは，指数近似式

\begin{align} y=ae^{bx} \end{align}

これらは非線形回帰分析によって求められたものではない。

例えば，累乗近似式は両対数グラフで線形となるように変数変換している。

\begin{align} \log y=\log a + b\log x \end{align}

対数部分を以下のように置換してみると良く分かると思う。

\begin{align} Y=A + bX \end{align}

このように変換された変数に対して最小二乗法を適用しているので，当然，元のデータに対する回帰式とは異なる。

同様に，指数近似も片対数変換して線形となるように，変数変換した上で，最小二乗法を適用している。

\begin{align} \log y=\log a + bx \end{align}

これらは，文字通り近似的にしか求められず，非線形回帰とはならないので注意が必要である。データに適合する関数を求める時，パソコンで非線形回帰が容易には計算できなかった時代の名残りとも言える便宜的方法である。この Excel グラフで近似曲線を求める方法で，指数回帰式や累乗回帰式を求めた，などと単純に学術論文に記すことは，今となっては，無知であること，恥ずかしいことなのである。ただし， Excel もバージョンによっては，計算法が異なる可能性があるので，その点は注意が必要である。

一方で，多項式回帰は線形回帰の問題であるのに，非線形回帰だと誤解している人もいる。

例えば，次の放物線（二次曲線）モデル

\begin{align} y=ax^2 + bx + c \end{align}

回帰式を求めるために，例えば，データ点（2, 3）を与えると，次のようになる。

\begin{align} 3=4a + 2b + c \end{align}

このように，パラメータの線形結合として表される式だと分かる。つまり，線形回帰か非線形回帰かは，関数が直線か曲線かの問題ではないのである。注意して欲しい。

Home