Excel両対数グラフで近似直線が曲線になる理由

井口豊（生物科学研究所，長野県岡谷市）
最終更新：2024 年 4 月 26 日

1. はじめに

Excel で両対数グラフにしたとき，近似直線を引くと曲線になる，という疑問がしばしば投げかけられる。Yahoo!知恵ノートの質問「エクセルで両対数グラフの近似直線が曲線」でも，累乗近似すれば直線になる，という単純な回答で終わってしまい，質問者もそれで納得してしまっている。おそらく本質的な部分を理解していないような気がする。以下に解説してみよう。

2. 両対数グラフで近似直線

以下のようなデータセット (x, y) を考える。なお，それらを自然対数変換したデータセット (LN(x), LN(y)) も，あとで利用するため算出しておく。

表1. Excel 両対数グラフのデータ

x	y	LN(x)	LN(y)
0.3	1	-1.204	0
0.9	0.6	-0.105	-0.511
1	3	0	1.099
2	2	0.693	0.693
5	30	1.609	3.401
9	10	2.197	2.303
15	150	2.708	5.011

まず， (x, y) を両対数グラフにプロットし，近似直線を挿入すると，次のようなグラフになる。

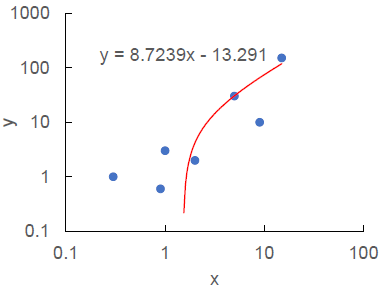図1. Excel 両対数グラフで近似直線を挿入．

確かに，直線になっていない。ここで，累乗近似を選択すると，次のようなグラフになる。

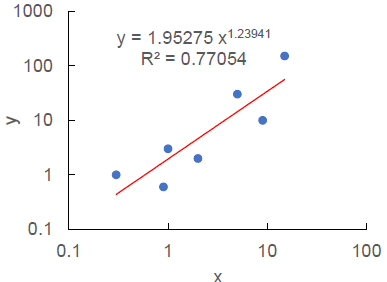図2. Excel 両対数グラフで累乗近似曲線を挿入．

こんどは直線になった。なお，ここでは，これまた誤解されがちな決定係数 R² も加えた。なぜ累乗近似で直線になるのか，以下のように説明される。

座標 (x, y) を対数変換した新たな座標 (X, Y) を考える。高校で学んだように，x を媒介変数とすると以下のように表される。便宜上，対数は， e を底とする自然対数を考える。

2 番目の式を整理すると次のようになる。

この数式について，表 1 で，対数変換したデータ LN(x), LN(y) を使って，直線近似を行うと，次のようなグラフになる。

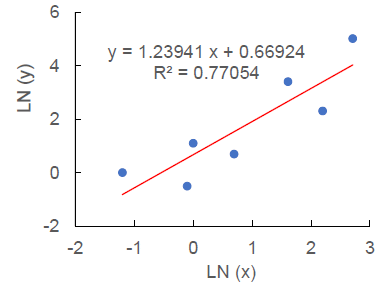図3. Excel 対数変換データを直線近似．

前述の式と全く同じであり，対数変換データに直線を当てはめ，それを累乗近似と称した結果が，両対数座標で直線となって表されているのである。

ここで注意してほしいのは，対数変換データの近似直線の決定係数 R² が，累乗近似の場合と全く同じである点である。つまり，Excel の場合，累乗近似曲線の R² を求めているのではなく，対数変換データの近似直線の R² を求めているのである（参照：Excelグラフ累乗，指数，多項式近似の論文記載の注意）。

そのページでも指摘したが，このような対数変換データの直線近似は，元データの累乗近似のベストフィットではないので注意が必要である。ベストフィットにするためには，非線形回帰を行うべきなのである。

話を戻すと，図 1 のニョロっとした曲線も，回帰直線の対数変換で考えることができる。図 1 の回帰直線の式を使って次のように変換する。

ここで， 1 番目の式を指数変換する。

それを 2 番目の式に代入する。

この回帰式をグラフ化してみるが，ここでは，統計解析ソフト R でやってみる。以下のようなスクリプトになる。

x<- c(0.3, 0.9, 1, 2, 5, 9, 15)
y<- c(1, 0.6, 3, 2, 30, 10, 150)

(mod<- lm(y ~ x))

# y = a*x + b
b<- coef(mod)[1]
a<- coef(mod)[2]

plot(
log(x), log(y), xlab="LN (x)", ylab="LN (y)",
xlim=c(-2, 4), ylim=c(-2, 8), pch=16, col="blue"
)

curve(log(a*exp(x)+b), col="red", lwd=2, add=TRUE)

legend(
 "topleft",
  expression(y == log(8.7239 * e^x - 13.291)),
  col="red", lwd=2, bty="n", cex=1.1
)

R の出力グラフは次のようになる。

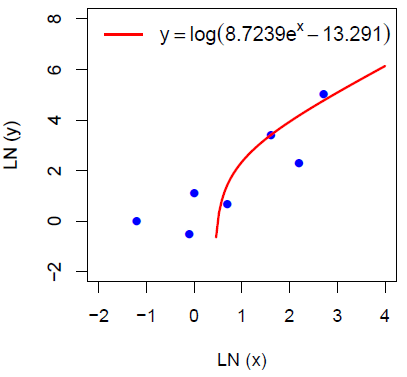図4. R による対数データと対数変換された近似直線プロット．

図 1 と全く同じグラフが，このような回帰式によって表されていることが確認できる。 Excel グラフの近似式を解説するならば，このくらいまでやってほしいものだ。