最小二乗と最小絶対値：ロバスト回帰で外れ値分析

井口豊（生物科学研究所，長野県岡谷市）
最終更新：2025 年 1 月 12 日

回帰式による直線や曲線の近似と言えば，通常は，最小二乗法（Least squares method）が使われる。 Excel のグラフや関数で使われる方法でもある。これは文字通り，回帰式で残差の二乗和（平方和）が最小となるように回帰式の係数を決定する方法である。これについては，以下のページを参照。

回帰と相関，知っているようで知らない，その本質：Excel の回帰分析を例として

一方で，二乗でなく絶対値の和が最小となるように係数を決定する方法を最小絶対値法（Least absolute value method）と呼ぶ。意外とこれが知られておらず，回帰や近似と言えば，最小二乗が当然だと思い込んでいる人も多い。

これらの方法は，異なる回帰式をもたらす。特に，外れ値を含む回帰式には，最小二乗法よりも最小絶対値法が適すると思える場合がある。つまり，後者はロバスト回帰（Robust regression）である。

ここでは，以下のような外れ値を含む 10 ペアの (x, y) データに対して，実際に，最小二乗近似と最小絶対近似によって，回帰式を求めてみよう。

x: 1, 2, 3, 4, 5, 6, 7, 8, 9 10
y: 6, 7, 8, 9, 0, 11, 12, 13, 14, 15

まず，最小二乗近似による回帰直線の適合を統計ソフト R で計算する。


#############
# データ
x<- 1:10
y<- 6:15
y[5]<- 0

# 最小二乗
f<- function(arg) {
  a<- arg[1]
  b<- arg[2]
  t<- a*x + b
  return(sum((y - t)^2))
}

# 結果
optim(c(1, 1), f)

# 同じ結果は， lm 関数で容易に得られる
lm(y~x)

# グラフ
a<- optim(c(1, 1), f)$par[1]
b<- optim(c(1, 1), f)$par[2]

plot(x, y, col="red")
curve(a*x+b, add=T, col="blue")
# 終了

################

回帰式は以下のとおり。

\begin{align} y = 1.061 x + 3.667 \end{align}

グラフは次の図 1 のようになった。

図 1. 外れ値がある場合の通常の最小二乗回帰

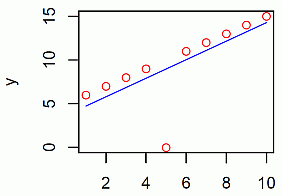
外れ値に引きずられ，なんとも中途半端な近似直線となっている。なお，通常は， lm 関数で容易に同じ結果が得られる。

次に，最小絶対値近似による回帰直線の適合を示す。


#############
# 最小絶対値
f<- function(arg) {
  a<- arg[1]
  b<- arg[2]
  t<- a*x + b
  return(sum(abs(y - t)))
}

# 結果
optim(c(1, 1), f)

# グラフ
a<- optim(c(1, 1), f)$par[1]
b<- optim(c(1, 1), f)$par[2]

plot(x, y, col="red")
curve(a*x+b, add=T, col="blue")
# 終了
################

回帰式は以下のとおり。

\begin{align} y = x + 5 \end{align}

グラフは次の図 2 のようになった。

図 2. 外れ値がある場合の最小絶対値回帰

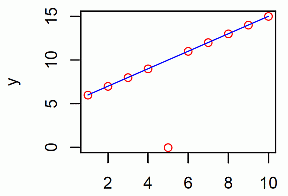
外れ値を，文字通り「外し」，残りのデータ点にピタリと一致した。最小絶対値法がロバスト回帰であると実感できる例である。

実際にパラメータが， a = 1, b = 5 となるのか， 3 次元グラフで確認してみよう。 z が，二変数 a, b の関数である以下の式を考える。

\begin{align} z = \sum\limits_{i=1}^n |y_i - (ax_i + b)| \end{align}

この z が最小となるような a, b を求めることになる。ここではフリーソフトである数式処理システム Maxima の lsum 関数を使って， 3 D グラフを見てみる。


#############
/* Least absolute value */
x: makelist(i, i, 1, 10)$
y: makelist(i, i, 6, 15)$
y[5]: 0$

f(a, b):= lsum(i, i, abs(a*x + b - y));

plot3d(f, [a, 0.5, 1.5], [b, 3, 7], [z, 10, 30], [plot_format,gnuplot], [grid, 50, 50]);
/* End */
################

グラフは以下のとおり。

図 3. 最小絶対値回帰予測値 z とパラメータ a, b の関係

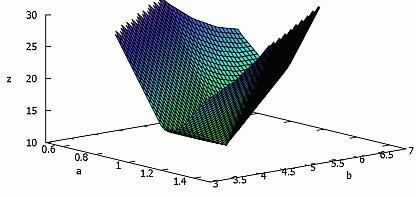
パラメータが， a = 1, b = 5 のとき， z が最小となることが見て取れる。

最小絶対値法の歴史と特徴に関しては，以下の文献が参考になる。

末吉俊幸（1997）
最小絶対値法による回帰分析
Journal of the Operations Research Society of Japan, 40(2): 261-275.

Home