母比率の検定:カイ二乗検定,二項検定,Z検定,1標本t検定,逆正弦変換検定
井口豊(生物科学研究所,長野県岡谷市)
最終更新:2022 年 3 月 11 日
1. はじめに
ここでは,母比率に対する 1 標本(1 群,サンプル数 1)適合度検定を, Excel と R を利用して解説している。 2 標本(2 群,サンプル数 2)の母比率の差の検定は,次のページ参照。
また,カイ二乗検定の下位検定としての残差分析は,次のページ参照。
さらに,多項の適合度検定は,次のページ参照。
ある町の男女の人数比が 1 対 1 と言えるか,というような母集団比率を検定する問題で, t 検定や Z 検定が使えることを知らない人が以外に多い。検定理論を理解していないため, Excel を十分に使いこなせてない人も多い。
母集団比率の検定問題が,そのデータを 0 と 1 のコード化(ダミー変数化)することによって平均を求めると,母集団平均の検定問題に帰着されることは,統計学の教科書,例えば,脇本(1984), p.125 にも書かれている。文献は,このサイト末尾の参考文献に一括してある。
では具体的に,どう分析するか,再度検討してみよう。なお,検定に使われる計算式自体はできるだけ省略し, Excel 関数と統計解析ソフト R を利用し結果を得ていく。例として,次のような問題を考える。
「既存の A 薬の効果は 65% である。新たな B 薬の効果は 43 例中 31 例であった。 B 薬は A 薬に比べて優れているといえるか?」
B の効果ありの母比率を p とすると,帰無仮説H0,対立仮説 H1 の設定は片側検定であるため,次のようになる。
H0: p = 0.65
H1: p > 0.65
2. カイ二乗検定(χ2 検定)
まず思い浮かぶのが, 適合度検定としてのカイ二乗検定である。 B の効果あり 31 例,効果なし 12 例の比率を,期待比率 0.65 : 0.35 と比べるのである。 2×2 分割表を使うと,次のようになる。
| 効果あり | 効果なし | |
|---|---|---|
| 観察値 | 31 | 12 |
| 期待値 | 27.95 | 15.05 |
ここで期待値は,全体の標本サイズに,それぞれの期待比率をかけて求められている。すなわち,
効果ありの期待値 = 43×0.65 = 27.95
効果なしの期待値 = 43×0.35 = 15.05
話は脇道にそれるが,用語の確認をしておきたい。
ここでのカイ二乗検定は,適合度検定であり, 1 標本検定である。つまり,標本数(サンプル数) 1
である。 1 標本は, 1 群とも呼ばれ,こちらのほうが,むしろ馴染み深い。つまり
群数 = 標本数
という関係がある。
一方で,測定値の数は,標本サイズ(サンプルサイズ) 43 である。
標本数(サンプル数)と標本サイズ(サンプルサイズ)を混同する人が非常に多いので,別ページで解説してある(参照:サンプル数とサンプルサイズ n は意味が違う)。
表 1 の検定は, Excel なら, CHITEST 関数を使い,括弧内に,順に,観察値と期待値のセルをドラッグすれば良い。
=CHITEST(B1:C1, B2:C2)
結果は,p = 0.3295
ただし,この場合,出力されるのは p 値だけなので,もしカイ二乗値を求めたければ, CHIINV 関数を用いて,自由度 1 として,上記 p 値を引数にすれば良い。
=CHIINV(p 値, 1)
統計解析ソフトRを使うと次のようになる。
chisq.test (c(31, 12), p=c(0.65, 0.35))
結果は
X-squared = 0.9509, df = 1, p-value = 0.3295
Excelと全く同じ結果となる。
最終的には,片側検定となるので
p = 0.3295/2
= 0.1647・・・(1)
片側 5% 水準で有意な差はない。
なお,いずれの計算でも, イェーツの連続性補正(Yates' continuity correction)は行われていない。この補正をしても,さらに p 値が大きくなるだけであり,ここでは意味がなく,詳しく触れない。
3. 二項検定
カイ二乗検定より,さらに正確な検定を使うなら, 二項検定が考えられる。効果の有無という事象は,コインの裏表と同じく,二項変数であると考えられるからである。
なお,カイ二乗検定の正確検定というと,すぐに Fisher 正確確率検定だと思い込んでしまうひとがいる。観察値と理論値の比較の場合, 2×2 分割表なら,二項検定が適用される。
Excelで二項検定を行うなら, BINOMDIST 関数を使う。本問のケースで,二項検定し, p 値を求めるなら,以下のような入力になる。
=1-BINOMDIST(30, 43, 0.65, TRUE)
最後の引数 TRUE は,累積確率であることを示す。効果ありの例数は, 31 でなく, 30 と入力。 つまり, X が 0~30 までの累積確率を,全体確率 1 から引いて, X が 31 以上となる確率を求めている。図にすると,以下のような右スソ面積に相当する確率(黄色部分)になる。
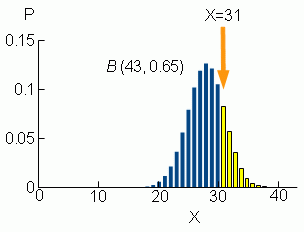
実際に,計算すると,
p = 0.2092・・・(2)
前述の (1) のカイ二乗検定の結果より少し大きな p 値で,もちろん片側 5% 水準で有意な差はない。
統計ソフト R を利用するならば,
binom.test (31, 43, alternative="greater", p=0.65)これで,同じ結果が得られる。
4. Z 検定
母比率の検定として Z 検定を行なう前に,中心極限定理の特別な場合として,ド・モアブル-ラプラスの定理(De Moivre–Laplace theorem)を考える必要がある。
ある事象 A が確率 p で起きる独立試行を n 回行ったとき, A が現れる回数 X は確率変数であり,それは二項分布 B(n,p) に従う。この確率変数 X は n が十分大きくなると,近似的に,平均 np,分散 np(1-p) の正規分布 N(np,np(1-p)) に従う。また,標本比率 X/n を考えると,それは近似的に正規分布 N(p,p(1-p)/n) に従う。
この定理を使い,帰無仮説 H0: p = 0.65 の下での検定を考える。つまり,「標本比率は 0.65 に等しい」,が帰無仮説になる。
すると, 標本比率(31/43)から 0.65 を引くと平均 0 の確率変数, それを分散 0.65(1-0.65)/43) の平方根,つまり標準偏差で割ると,標本比率は標準化, その結果となる確率変数 Z は,標準正規分布 N(0,1) に従う。
\[ Z=\frac{\frac{31}{43}-0.65}{\sqrt{\frac{0.65(1-0.65)}{43}}} \]この統計量を用いて検定すれば良い。いわゆる Z 検定(Z-test)である。
実際に計算すると,
Z = 0.97516
となる。
この片側 p 値は, Excel ならば,次のように求める。
= 1-NORMSDIST(0.97516)
結果は,
0.1647・・・(3)
前述の (1) のカイ二乗検定と同じ結果となった。
これは当然である。 標準正規分布 N(0,1) に従う確率変数 Z の二乗,つまり, Z2 は,自由度 1 の χ2 分布になるのである。
統計ソフト R を利用するならば,
prop.test(31, 43, correct=F, p=0.65, alternative="greater")これで,同じ結果が得られる。
5. t 検定(1 標本)
冒頭述べたように,母比率の検定には t 検定も適用できる。そのためには,まず効果の有無にそれぞれ, 1 と 0 の数字コード(numerical code)を割り当て,ダミー変数(dummy variable)とするのである。
すると, B の平均 m は,
m = (31*1+12*0)/43
= 31/43
平均値が効果有りの比率そのものだと分かる。これを 0.65 と比べ,片側検定すれば良いのである。
統計ソフト R を使うなら,1標本 t 検定(片側)で次のようにする。
x<- rep(0:1, c(12, 31)) # 0が12個,1が31個 t.test (x, mu=0.65, alternative="greater")
結果は,
t = 1.0248, df = 42, p-value = 0.1557・・・(4)
これを Excel を使ってするには,対応のある t 検定を利用する。対応のある t 検定は,本質的に 1 標本(1 群)問題であるが,それを知らない人も結構いる。 R の解説で, 1 標本検定の項目に,対応のある t 検定が取り上げられているページがあるが,まさに正しい扱いなのである。
対応のある t 検定とは,対応のあるデータを引き算して 1 群とし,それがある特定の平均,例えば,平均 0 の分布となるかどうかを検定している。例えば,以下のような例を計算するとよく分かる。ここでは, R を使ってみる。
まず,以下のような, 2 群(2 標本)の対応のある t 検定を計算する。
x<- c(58, 57, 60, 58, 59) y<- c(52, 49, 51, 57, 55) t.test(x, y, paired=TRUE)
結果は,
t = 3.9017,df = 4,p-value = 0.01752
一方,これらのペアデータを引き算して1群 z を作り,平均 0 に対して, 1 標本 t 検定する。
z<- x - y t.test (z, mu=0)
結果は,
t = 3.9017, df = 4, p-value = 0.01752
対応のある t 検定の結果と一致する。
さらに,次のように全て 0 からなる 1 群 w を考え, z と w で対応のある t 検定を行う。
w<- c(0, 0, 0, 0, 0) t.test(z, w, paired=TRUE)
結果は,
t = 3.9017, df = 4, p-value = 0.01752
前述の二つの結果と一致する。
これで,「対応のある t 検定とは,対応のあるデータを引き算して 1 群とし,それが平均 0 の分布となるかどうかを検定している」,ことが理解できると思う。
Excel で分析するためには,まず, 0 が 12 個, 1 が 31 個のダミー変数を作り,それぞれに, 0.65 というデータを対応させる。これらを,次の表2のように,ずらっと 1 列に並べればよい。
| n | A | B |
|---|---|---|
| 1 | 0 | 0.65 |
| 2 | 0 | 0.65 |
| 3 | 0 | 0.65 |
| ・ | ・ | ・ |
| ・ | ・ | ・ |
| 41 | 1 | 0.65 |
| 42 | 1 | 0.65 |
| 43 | 1 | 0.65 |
= TTEST (A1:A43, B1:B43, 1, 1)3 番目と 4 番目の引数 1 は,それぞれ,片側検定で,対応ある検定であることを指定している。
その結果は,
0.1557・・・(5)
つまり,統計ソフト R を用いた 1 標本 t 検定の p 値 (4) と一致する。
Excel を用いた母比率に関する 1 標本 t 検定は,このようにするが,意外と,入力方法も知らない人が多い。
6. 逆正弦変換 Z 検定
逆正弦変換(arcsine transformation, 角変換)を利用した分散分析に関しては,例えば,日本女子大・岡本安晴のウェブページ,比の差の分散分析を参照してほしい。ここから,計算プログラムもダウンロードできる。
また,逆正弦変換を利用した分散分析の参考文献としては,岩原(1964)が挙げられる。
逆正弦変換は,角度の単位に度(°)を使っても,ラジアン(rad)を使っても良いのだが,ここでは一般に馴染み深い単位として度を用いて議論を進める。前述の岩原(1964)でも,度を用いて逆正弦変換が説明されている。
ある比率 p を,逆正弦変換によって,角度 d に直したとすると以下のような式になる。
\[ d=\arcsin(\sqrt{p}) \] または,\[ d=\sin^{-1}(\sqrt{p}) \]
Excelならば,以下のようにすれば,逆正弦変換した上で,度(°)に直せる。
=DEGREES(ASIN(SQRT(p)))
表 1 のデータで,効果ありの比率を逆正弦変換した結果が,次の表 3 である。
| 効果あり比率 | 逆正弦変換 | |
|---|---|---|
| A | 0.65 | 58.111 |
| B | 31/43 | 53.729 |
逆正弦変換したデータは,正規分布になり,その分散 σ2 は,度(degree)を単位として,次のようになる。
\[ \sigma^2=\frac{1}{4n}\left ( \frac{180}{\pi} \right )^2deg^2\approx \frac{821}{n}deg^2 \]この 821 は,しばしば定数のように用いられるので注意が必要である。例えば,印東(1962), p.20 右段の解説がそれである。
正規分布となった逆正弦変換値の差の検定には,前述のように Z 検定が使える。岡本の説明のように,逆正弦変換の分散分析には, χ2 値を使う。しかし,本問の場合は,
自由度 = 2 - 1 = 1
なので, χ2 値の平方根が,正規分布となることからも, Z 検定が使えると分かる。したがって, Z は次のように表せる。
この片側 p 値を Excel で求めるときは,次のようにする。
P =1-NORMSDIST(1.003)
結果は,
0.1579
この結果は,前記の t 検定の結果と,ほぼ同じとなり,実質的には,逆正弦変換を利用した Z 検定も利用できると分かる。
7. まとめ
以上,5種類の検定結果を次の表 4 に示した。
| 検定 | p |
|---|---|
| カイ二乗検定 | 0.1647 |
| 二項検定 | 0.2092 |
| Z 検定 | 0.1647 |
| 1 標本 t 検定 | 0.1557 |
| 逆正弦変換 Z 検定 | 0.1579 |
正確さという点から言えば,二項検定が良いのだが,本問に限って言えば,どれを使っても実質的問題はないと言える。 t 検定の p 値が,カイ二乗検定や Z 検定の p 値に近いが,これは, t 分布も標本サイズが大きくなると正規分布に近づくことに起因している。
参考文献
印東太郎(1962) サーストンの心理尺度構成法. 日本音響学会誌 18(1): 16-22.
岩原信九郎(1964) ノンパラメトリック法―新しい教育・心理統計. 日本文化科学社
脇本和昌 (1984) 統計学―見方・考え方. 日評数学選書