比率の差 Z 検定の注意点：統合比率を使う理由

井口豊（生物科学研究所，長野県岡谷市）
最終更新: 2024 年 11 月 11 日

PDF version
DOI: 10.5281/zenodo.14064942

母比率の差の検定（独立2群の比率の差の検定）として， Z 検定を行う場合，基本となる検定統計量は以下の式である。

\begin{align} Z = \frac{p_1-p_2}{\sqrt{\frac{p_1(1-p_1)}{n_1} + \frac{p_2(1-p_2)}{n_2}}} \end{align}

ここで，n₁， n₂ は 2 群それぞれの標本サイズであり，p₁， p₂ は，それぞれの標本比率である。この Z が標準正規分布にしたがうことを利用して検定する。

それぞれの標本で観察された属性の個数を x₁， x₂ とすれば，p₁， p₂ は，以下のように書ける。

\begin{align} p_1 = \frac{x_1}{n_1} \\ p_2 = \frac{x_2}{n_2} \end{align}

しかしながら，このとき，帰無仮説が 2 群の母比率に差がない，という場合は，分母には，p₁， p₂ を別々に使わず，以下のような標本比率をプールした統合比率（pooled proportion） p を用いる。

\begin{align} p = \frac{x_1+x_2}{n_1+n_2} \end{align}

ここで， x₁， x₂ は，それぞれの標本で観察された属性である。したがって， Z は以下のようになる。

\begin{align} Z = \frac{p_1-p_2}{\sqrt{p(1-p) \left(\frac{1}{n_1} + \frac{1}{n_2} \right)}} \end{align}

なぜ，統合（プールすること，pooling）が必要なのか，日本語の教科書やウェブページでは，ほとんど解説していない。海外の例では，Saint Mary's College の Charles Peltier による以下の解説が詳しい。

Why Do We Pool for the Two-Proportion z-Test?

そのページ真ん中付近に，統合する理由が明確に述べられている。

We have done this not because it is more convenient....... nor because it reduces the measurement of variability..... but because it gives us the best estimate of the variability of the difference under our null hypothesis that the two sample proportions came from populations with the same proportion.

分散を統合するのは，簡便な方法とするためではなく，バラツキを小さくするためでもなく，母比率（population proportion）が等しいという帰無仮説の検定では，それが比率の差の分散として最良な推定量となること書かれている。

これは，統合比率を使った Z 検定が，カイ二乗検定と同等なものであることからも推察される（参照ページ：比率の差：Z 検定とカイ二乗検定は同等である）。同じデータに対して，どちらの検定で計算しても，同じ有意確率が算出される。

母比率の差の検定は，統計検定 2 級の出題範囲であり，大学 1，2 年レベルの問題なのだが，なぜ統合比率が必要かを理解していない人も多いようだ。

言葉でゴチャゴチャ説明するより， R でシミュレーションして確認してみよう。

ここでは，母比率を 0.2 と設定して， 2 群の標本サイズを以下のように変化させる。
n₁: 5, 10, 20, 30, 40, 50
n₂: 10, 20, 30, 40, 50, 60

統合 Z 検定と非統合 Z 検定を行う。帰無仮説を適切に棄却できるならば，有意確率は 0.05 になる。


# R スクリプト
p<- 0.2 # 母比率

# シミュレーション比の差
dat<- c(0, 1) # 属性の有無 二値データ

k<- 100000 # 抽出反復数  
pz1<- as.numeric(NULL)
pz2<- as.numeric(NULL)

# 標本サイズ
n1<- c(5, 10, 20, 30, 40, 50)
n2<- c(10, 20, 30, 40, 50, 60)
N<- n1+n2

set.seed(101)

for (i in 1: 6) {

pr<- replicate(k, {

# グループ1の標本
s1<- sample(dat, n1[i],
 replace=T, prob=c(p, 1-p))
a1<- length(s1[s1==0]) # 属性有り個数 
p1<- a1/n1[i] # グループ1標本比率

# グループ2の標本
s2<- sample(dat, n2[i],
 replace=T, prob=c(p, 1-p))
a2<- length(s2[s2==0]) # 属性有り個数
p2<- a2/n2[i] # グループ2標本比率

d<- abs(p1-p2) # 比率の差

# 2群の属性，統合比率
pp<- (a1+a2)/(n1[i]+n2[i])

# 統合 Z 検定
z1<- d/sqrt(pp*(1-pp)*(1/n1[i]+1/n2[i]))

# 非統合 Z 検定
z2<- d/sqrt(p1*(1-p1)/n1[i] + p2*(1-p2)/n2[i])

# 各 P 値
c(pnorm(z1, lower=F)*2,
 pnorm(z2,lower=F)*2
)

})

# 統合 Z 検定 5%水準の棄却率
pz1[i]<- length(pr[1, ][pr[1, ]<=0.05])/k
# 非統合 Z 検定 5%水準の棄却率
pz2[i]<- length(pr[2, ][pr[2, ]<=0.05])/k

}

# グラフ
par(mar = c(5, 5, 4, 8),
    ps = 18)

ttl<- "プール，非プール比の差 Z 検定"

# プールZ検定 棄却率変動
plot(N, pz1, main=ttl, type = "b",
   xlim=c(10, 120), ylim=c(0, 0.2),
   col="blue", pch=1,
   xlab="全体の標本サイズ（n1+n2）",
   ylab="5%水準の棄却率")

# 非プールZ検定 棄却率変動
lines(N, pz2, type = "b", col="red", pch=4)

abline(h = 0.05) # 5%有意水準のライン

legend("topright",
    c("Unpooled Z test", "Pooled Z test"),
    col=c("red", "blue"), pch=c(4, 1),
    lw=2, bty="n")

# シミュレーション終了

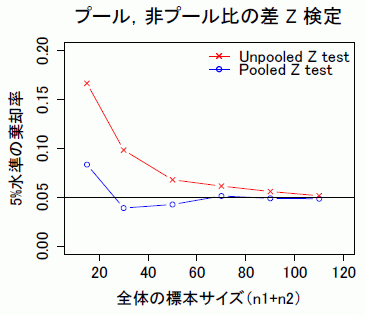
プール，非プール比の差 Z 検定

図 1. プール，非プール比の差 Z 検定

結果のグラフを見て，重要なことが二つあるのに気づく。まず，第一に，Z 検定は正規近似を行っているため，標本サイズが小さいと適切な結果が得られない，ということである。第二に，やはり統合 Z 検定のほうが適切な p 値が得られる，ということである。

大学などの授業でも，なぜ統合比率が必要かを，きちんと説明すべきであろう。

Home