多項適合度検定: 3 項以上の正確検定,近似カイ二乗検定,多重比較
井口豊(生物科学研究所,長野県岡谷市)
最終更新: 2023 年 12 月 12 日
1. はじめに
度数(人数や回数)で 3 項以上の適合度検定として,正確検定(exact test)に使われるのが,多項検定(multinomial test)である。 3 項以上と書いたが,正しくは 2 項以上であり, 2 項(二値データ)の場合が良く知られた 二項検定(binomial test)になる。したがって,多項検定の,いわゆる下位検定として,二項検定による多重比較が用いられる。二項検定に関しては,以下のサイト参照。
正確検定と言うと,独立性検定としての Fisher 正確検定と混同されやすいので,注意が必要だ。それは別サイトに書いた。
近似的な適合度検定として使われるのが,これも良く知られたカイ二乗検定である。ただし,期待度数(理論度数)が小さいと,正しく計算できない。それは独立性検定でも,適合度検定でも同様である。
適合度検定のデータとして使われる代表例が,メンデルのエンドウ豆の交配実験の結果である。それに関しては,例えば,儀我(2014) p.116 適合度検定を参照しほしい。 文献情報は,最後の参考文献に一括した。
本サイトでは,もっと身近な例として,サイコロの目が出る回数の適合度検定を扱う。
2. データ: サイコロの目が出た数
次の表 1 のように集計された 1 から 6 のサイコロの目が出た回数が同数(同比率)であるかどうか,統計ソフト R を使い検定する。
3. 適合度検定(正確多項検定と近似的カイ二乗検定)と多重比較
#############
# サイコロの目が出た回数データ
x<- c(
"1" = 0,
"2" = 10,
"3" = 6,
"4" = 4,
"5" = 5,
"6" = 5
)
# サイコロの目
score <- names(x)
# 目が出る比率
n<- sum(x)
Ratio<- x/n
# 95% 信頼区間上限
ci.1<- function (x) {
binom.test(x, n)$conf.int[1]
}
CI.low<- as.numeric(
tapply(x, score, ci.1)
)
# 95% 信頼区間下限
ci.2<- function (x) {
binom.test(x, n)$conf.int[2]
}
CI.up<- as.numeric(
tapply(x, score, ci.2)
)
# データフレーム
g.df<- data.frame(
Face = factor(names(x)),
Ratio,
CI.low,
CI.up
)
head(g.df)
# グラフ
library(ggplot2)
g<- ggplot(
g.df,
aes(
x = Face, y = Ratio
)
) +
geom_errorbar(
aes(ymin = CI.low, ymax = CI.up),
width = 0.1, color = "blue"
) +
geom_point(size = 2, color = "blue") +
ylim(0, 0.6) +
ggtitle(
"Ratio with 95% CI"
)
plot(g)
# 近似的カイ二乗検定
pc<- chisq.test(x)
pc
# 近似的カイ二乗検定 p 値
round(pc$p.value, 3)
# 正確多項検定
library(rstatix)
pm<- multinom_test(x)
pm
# 正確多項検定 p 値
round(pm$p, 3)
# 正確二項検定による多重比較(Holm 補正)
pb<- pairwise_binom_test(
x,
p.adjust.method = "holm"
)
# 詳細な結果
pb
# 多重比較 Holm 補正 p 値
data.frame(
Face.pair_1 = pb$group1,
Face.pair_2 = pb$group2,
P.adj = round(pb$p.adj, 3)
)
################
結果は以下の通りである。 グラフと検定結果の抜粋を示す。
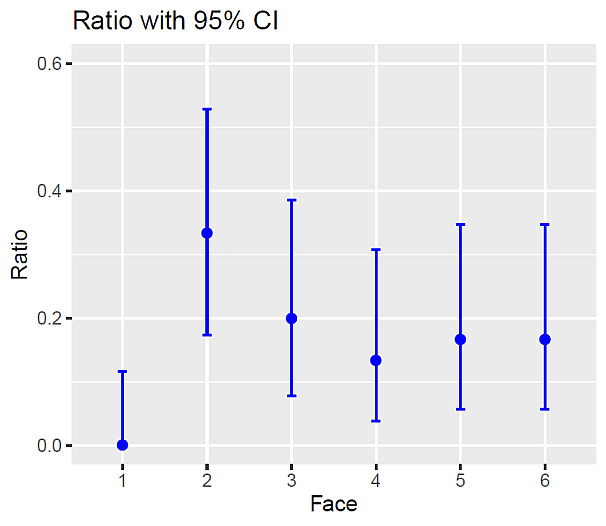
################################################
# カイ二乗検定 p 値
0.065
# 正確多項検定 p 値
0.031
# 正確二項検定による多重比較(Holm 補正)
Face.pair_1 Face.pair_2 P.adj
1 1 2 0.029
2 1 3 0.438
3 1 4 1.000
4 1 5 0.812
5 1 6 0.812
6 2 3 1.000
7 2 4 1.000
8 2 5 1.000
9 2 6 1.000
10 3 4 1.000
11 3 5 1.000
12 3 6 1.000
13 4 5 1.000
14 4 6 1.000
15 5 6 1.000
################################################
近似検定であるカイ二乗検定では,全体として有意差が無い(p = 0.065)が,正確多項検定では有意差が見られる(p = 0.031)。
正確二項検定による多重比較(Holm 補正)では, 1 と 2 の目が出た回数の間に有意差が認められた(p = 0.029)。