Fisher 正確検定の多重比較， R と EZR を例にして

井口豊（生物科学研究所，長野県岡谷市）
最終更新： 2023 年 2 月 21 日

1. 統計ソフト R による Fisher 正確検定

　男女とか，はい・いいえとか，いわゆる二値データの度数比（人数比や個数比）の検定に使われるのが， Fisher 正確検定であり，独立性の正確検定である。近似的な検定であるカイ二乗検定が，独立性検定にも，適合度検定にも使われるため，しばしば誤解されるが，適合度検定の正確検定は，多項検定（二項検定も含む）となるので注意が必要である。

多項適合度検定: 3 項以上の正確検定，近似カイ二乗検定，多重比較

例えば，以下の表 1 のようにクロス集計された 3 群， A, B, C の男女別の人数データで，男女比が等しいか検定する。

表 1．3×2 分割表（3 群の男女別人数）
群	男	女
A	7	16
B	14	8
C	23	5

統計ソフト R の Fisher 正確検定では，以下のようなスクリプトになる。


###############
# データ
dat<- matrix(c(
 7, 16,
 14, 8,
 23, 5
), ncol=2, byrow=T)

## Fisher 正確検定
fisher.test(dat)

####################

結果は以下の通り。

p = 0.0009

これが通常の Fisher 正確検定の結果である。以前は，この検定が 2×2 分割表（クロス表）だけに使われていたが，現在のパソコンやソフトでは，それより大きな分割表でも計算可能となっている。

2. Fisher 正確検定の多重比較， R と EZR の利用

表 1 のデータを，それぞれの群間で，いわゆる多重検定する。

R 本体で計算する場合は，パッケージ RVAideMemoire の中の fisher.multcomp 関数が使える。 fisher.multcomp 関数のマニュアルを見ると分かるが，多重比較法として， Bonferroni, Holm, Benjamini and Hochberg などが使える。

表 1 のデータに対して， Holm 法で多重比較するスクリプトは，以下のようになる。


###############
# 利用パッケージ
library(RVAideMemoire)

## データ
dat<- matrix(c(
 7, 16,
 14, 8,
 23, 5
), ncol=2, byrow=T)

## Fisher 正確検定の多重比較
fisher.multcomp(dat, p.method="holm")

################

結果は，以下のようになる（一部抜粋）。

   A             B
B 0.075364     -
C 0.001346 0.197

P value adjustment method: holm

このような多重検定を EZR でやってみよう。まず，
統計解析 → 名義変数の解析
→ 分割表の直接入力と解析
とタブをたどっていき，下図のようにデータ入力し， OK をクリックする。

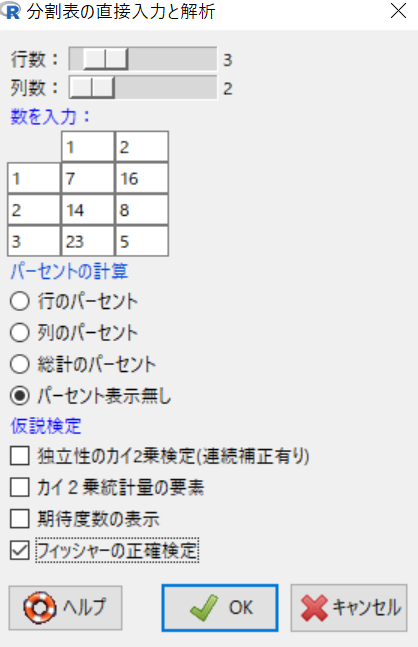図 1. EZR クロス集計表での入力画面

このとき， EZR では，入力データが， ,Table という名称の行列に格納されている。さらに， EZR では， pairwise.prop2.test 関数を使って多重検定する。これを Holm 法で計算すると，以下のようなコードになる．もちろん，前述のように，様々な方法が使える。


###############
pairwise.prop2.test(.Table, p.adj="holm", test.function=fisher.test)

################

このコードを EZR の上の画面「Rスクリプト」に書き込んで，マウスで選択し，「実行」をクリックすると，下の図 2 のように出力される。

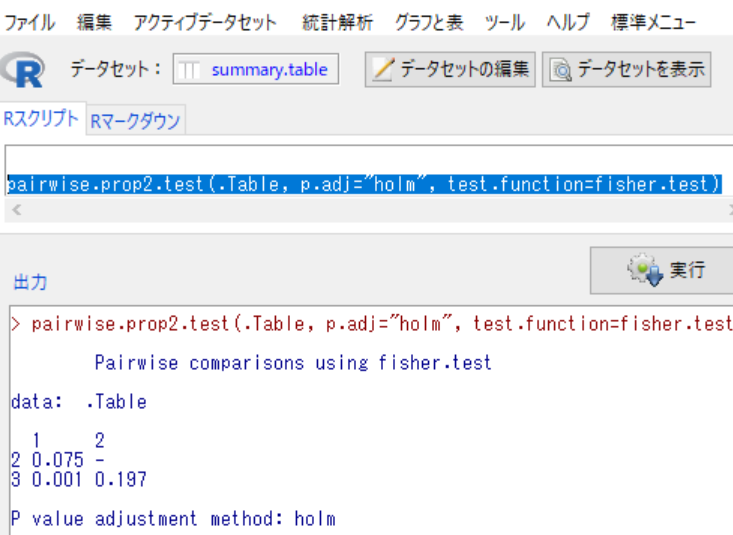図 2. EZR による Fisher 正確検定の多重比較

前述の fisher.multcomp 関数の結果と同じ数値で，出力桁数が異なるだけであることが分かる。

3. Fisher 正確検定の全体検定のあとで多重比較しない

Fisher 正確検定でデータ全体を検定し，それが有意であれば，多重比較する，という手順は不適切である。何も考えずに，ルーチンがごとく，こういう手順で検定する例が非常に多いので，分散分析を例にして，以下のページで注意を促した。

分散分析の下位に多重検定を置くな

Fisher 正確検定やカイ二乗検定の場合も同様であり，群間の比較に関心があるならば，最初から多重比較するべきである。

例えば，以下の論文では， Silicone Breast Implant の回転について，エキスパンダーの種類を Mentor, Allergan 社製品を用いて比較した研究である。

浜永真由子・森弘樹・植村法子・岡崎睦 (2017)
乳房インプラントの回転エキスパンダー・インプラントの選択との関連性について
Oncoplastic Breast Surgery 2(3): 78-83.

この論文の図 1 では，最初から群間の多重検定の結果だけ示し，有意差が無いことを記述している。このようにすれば良いのである。全体で有意差があったら多重比較という手順は望ましくない。ちなみに，この論文の表 1 でも，平均の比較で， Tukey 多重検定の結果だけ示している。

この問題で， Fisher 正確検定に関して詳細は，以下のページ参照。

Fisher 正確検定の後に多重比較するな

Home