分散分析の下位に多重検定を置くな

井口豊（生物科学研究所，長野県岡谷市）
最終更新： 2022 年 5 月 17 日

1. はじめに

分散分析 ANOVA の結果，それが有意になると，下位検定あるいは事後検定（post hoc test）として多重検定が行われる（行われるべきだ？），という短絡的な説明がネット上で見受けられる。分散分析と多重検定は，それぞれ異なる目的であり，別々に独立に行われても良いのであるし，そうすべきである状況も多い。意外と，そういう解説は少ない。

この問題について，統計ソフトの解説としては珍しく的確に指摘しているのが，エクセル統計（BellCurve）のブログ「検定の多重性」である。

教科書によっては多重比較が分散分析の下位検定（post-hoc test）でしかないような書き方をしているものもありますが、これは誤解です。

まさに，このような現状なのである。そのページを読んでいくと，その原因も書かれている。

エクセル統計も含め多くの統計ソフトはの分散分析の機能と同じ場所にオプションとして多重比較を備えています。

分散分析と多重検定は，統計ソフトの便宜的な仕様としてセットになっているのだが，それがいつのまにか，分散分析で有意差が認められたら，その後，多重検定という「手順」だと誤解されているのである。

統計ソフトの解説として，英文で参照して欲しいのが， GraphPad (Prism) の解説 If one-way ANOVA overall has P>0.05, is it possible for all the multiple comparisons tests to be "not significant"? である。

Since multiple comparison tests are often called 'post tests', you'd think they logically follow the one-way ANOVA. In fact, this isn't so.

前述のエクセル統計のブログと同様な指摘をしていることが分かる。そのページを読むと，分散分析が有意でも多重比較が有意とは限らないし，逆に，分散分析が有意でなくても多重比較が有意となることもある，と書かれている。全くそのとおりなのだが，大学の授業や卒論や学位論文指導などでも，そのように教えられることは少ないようだ。むしろ逆に，「分散分析が有意になったから事後検定として多重比較しなさい」と学生に指示する教員さえいるようだ。

GraphPad による解説ページの下のほうに次のように書かれている。

More often, your experimental questions are more focused and answered by multiple comparison tests (post tests). In these cases, you can safely ignore the overall ANOVA results and jump right to the post test results.

元々，多重比較に興味があるのなら，分散分析の結果は無視することが出来るのである。何でもかんでも，まず分散分析という考え方は改めて，多重検定から入っていくような手順の研究も進めてほしいところである

2. 単独検定と事後検定： Tukey 検定を使った例

分散分析で有意差が認められた後に事後検定として多重検定する場合と，最初から単独検定（分散分析とセットにせず）として多重検定する場合の有意確率を比較してみよう。

ここでは，しばしば使われる多重検定法である Tukey 検定（Tukey HSD, honestly significant difference）を取り上げる。標準正規母集団から，同じ大きさ 20 の三つの標本（サンプルサイズ 20，サンプル数 3）を取り出す操作を 10 万回繰り返して， 5 ％水準 (α = 0.05) で棄却される比率を調べてみた。すなわち，第一種過誤率 (Type I error rate) を調べた。

#### スクリプト開始

n1 <- n2 <- n3 <- 20

np <- 0
np.anov <- 0
anova.p <- as.numeric(NULL)
k <- 100000
group <- factor(rep(1:3, c(n1, n2, n3)))

for (i in 1:k) {  

  x1 <- rnorm(n1, mean = 0, sd = 1)
  x2 <- rnorm(n2, mean = 0, sd = 1)
  x3 <- rnorm(n3, mean = 0, sd = 1)

  res <- aov(c(x1, x2, x3) ~ group)

  anova.p[i] <- anova(res)$Pr[1]

  pt <- TukeyHSD(res)$group[, 4]

  if (pt[1] < 0.05 || pt[2] < 0.05 || pt[3] < 0.05) {
   np <- np + 1
  }

  if (anova.p[i] < 0.05 && (pt[1] < 0.05 || pt[2] < 0.05 || pt[3] < 0.05)) {
   np.anov <- np.anov + 1
  }
}

hist(anova.p)

# 5% 水準での棄却率
# Tukey 検定のみ
rnp <- np/k

# ANOVA 有意後，Tukey 検定
rnp.anov <- np.anov/k

barplot(
 c(rnp, rnp.anov), ylim = c(0, 0.06), col = "#0080ff",
 names.arg =c("Tukey test only", "Tukey test after ANOVA"),
 ylab = "Type I error rates with alpha level 0.05"
)
abline(h = 0.05, col = "red", lwd = 2)

### スクリプト終了

結果は，次の図 1 のとおりである。

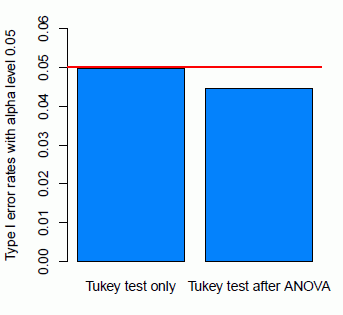
分散分析に有意差が認められた後に，事後検定として， Tukey 多重比較検定を行うと，正しく棄却されないことが一目瞭然である。

3. 他の検定でも同じ

当然だが，他の検定でも，下位検定（事後検定 post hoc test）が多重検定ではなく，全体の検定と多重比較検定は，それぞれ異なる目的で独立に検定される。

母比率の比較の検定として，しばしば使われる Fisher 正確検定の場合も，その点を別ページで言及した。

• Fisher 正確検定の後に多重比較するな

上記ページと内容が一部重複するが，以下のページも参照。

• Fisher 正確検定の多重比較，R と EZR を例にして

そのページの，特に， Fisher 正確検定の全体検定のあとで多重比較しないを参照してほしい。