logo
生物科学研究所 井口研究室
Laboratory of Biology, Okaya, Nagano, Japan
Home

母比率の差: カイ二乗検定， z 検定，ロジスティック回帰

井口豊（生物科学研究所，長野県岡谷市）
最終更新： 2023 年 1 月 16 日

1. はじめに

例えば，男女に，はい・いいえ，という二件法アンケートを実施して，その結果をまとめた 2×2 クロス集計表データ（表 1）を考えてみる。

表 1．質問クロス集計
男女
はい2335
いいえ2518

このような場合，男女のはい・いいえ比率を比較するとき，代表的なノンパラメトリック検定に，いわゆるカイ二乗検定がある。

このカイ二乗検定が，実は，母比率の差のパラメトリック検定である z 検定と全く同じ式で表されることは，別ページで証明した。

しかしながら，男・女もはい・いいえも二値データであり，ダミー変数 0, 1 にすると，一般化線形モデル（GLM）ロジスティック回帰分析も適用できるのである。

ここでは， R を使い，シミュレーションでカイ二乗検定とロジスティック回帰の p 値を比較してみた。

2. カイ二乗検定とロジスティック回帰分析の p 値の変化

セルのサンプルサイズ を 15 から 40 で変化させて，両検定の p 値を比較した。

以下が， R スクリプトである。 


#############

k<- 1e+2 # 標本取り出し反復回数

p<- replicate(k, {

  # 度数データ
  x<- sample(15:40, size = 4, replace = T)

   # 群分け
   group<- factor(rep(
      c("male", "fmale"), 
      c(sum(x[1:2]), sum(x[3:4]))
      ))

  # ダミー応答変数
  res<- factor(rep(rep(c("Yes", "No"), 2), x))

  c(
   # カイ二乗検定 p 値
   chisq.test(
     matrix(x, ncol = 2),
     correct = FALSE)$p.value,

    # ロジスティック回帰 p 値
    summary(glm(
      res ~ group, family = binomial(link = "logit")
          ))$coef[2, 4]
   )

})

p.chisq<- p[1, ]
p.logit<- p[2, ]

par(oma = c(3, 3, 2, 2))

plot(
 p.chisq, p.logit,
 xlab = "Chi-square test",
 ylab = "Logistic regression",
 main = "P value",
 col = "blue",
 xlim = c(0, 1), ylim = c(0, 1)
)
abline(0, 1, col = "red")

################

結果は，次の図 1 のとおりである。

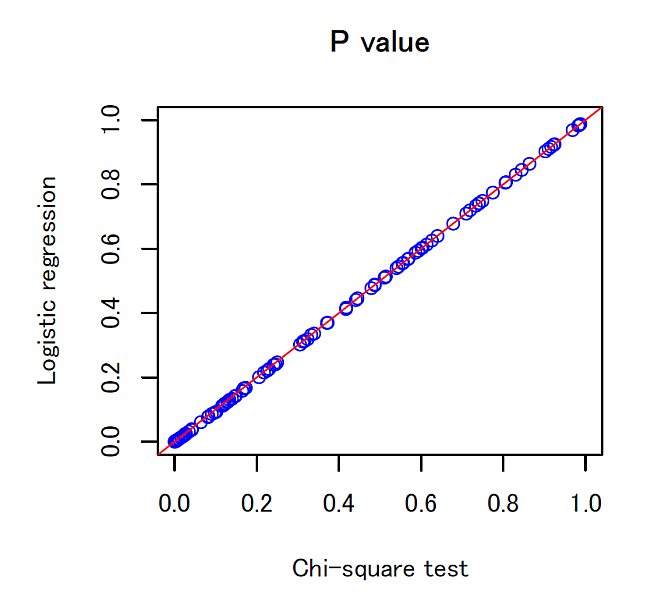
カイ二乗検定と分散分析 p 値

図 1. p 値の比較: カイ二乗検定とロジスティック回帰分析

カイ二乗検定とロジスティック回帰分析の p 値が，ほぼ一致することが分かる。

関連サイト

Home