小標本 t 検定の誤解：中心極限定理と一般化線形モデル

井口豊（生物科学研究所，長野県岡谷市）
最終更新：2022 年 12 月 6 日

1. はじめに

小標本なら t 検定という言説をネット上でチラホラ見かけた。どうやら，元を辿っていくと，行き着く先の一つが，西内啓　著「統計学が最強の学問である（実践編）」（ダイヤモンド社）であるらしい。

確かに，11 章「少ないデータのための t 検定とフィッシャーの正確検定」（p.152 ～）には，小標本ならば t 検定という説明が書かれている。しかし問題は，どのような母集団から取り出した標本なのか，それが明記されていないことである。

この部分で言及されている，t 検定を発明した W. S. Gosset の論文は pdf として読める。

Student (1908)
The Probable Error of a Mean
Biometrika: 1-25.

それを読むとわかるが，教科書にもしばしば書かれているとおり，正規分布母集団を仮定した検定なのである。

もちろん，標本サイズが大きくなるにつれて，母集団が正規分布でなくても，その平均値の分布は漸近的に正規分布に従う。そのことは，本書の『「現代統計学を支える「中心極限定理」』（p.63 ～）」という項目で，類書に例を見ないほど細かく解説されている。しかし， t 検定の本来の前提条件は，正規母集団を仮定しており， Gosset に言及するなら，その仮定を述べる必要がある。

そのことに関連して，t 検定を適用できる標本サイズについても，「さすがにサンプルが4というのは行き過ぎ」とか，「数十件程度のデータ」とか述べているが，これもまた母集団の種類によって異なる。

2. t 検定のシミュレーション，母集団が正規分布の場合

Gosset の仮定の下に，統計ソフト R を使って，実際にシミュレーションで t 検定の性質を調べてみよう。まず，標準正規分布（平均 0，標準偏差 1）の母集団から，大きさ 4 の標本（サンプルサイズ 4）を 10 万回取り出したとして，次の3点を調べてみた。ここで行なったのは，1 標本検定（サンプル数 1）の検定である。

1. 平均値 m の度数分布
2. 帰無仮説 H0: m = 0 に対して，5％有意水準で t 検定を行なったときの棄却率 p
3. 棄却率 pの度数分布

これは中心極限定理を考える必要はなく，正規分布の再生性から，平均値は，平均 0，標準偏差 1/sqrt(4) の正規分布となる。したがって，5％有意水準で t 検定を行なえば，当然，棄却率も 5 ％であり，その頻度分布は一様になる（どこでも同じである）はずである。

以下に， R によるシミュレーションのスクリプトを書く。

# 正規母集団からの標本（n=4）に対して t 検定

k<- 100000 # 標本取り出し反復回数
n<- 4 # 標本サイズ

r<- replicate(k, {

 x<- rnorm(n, mean=0, sd=1)
 c(mean(x), t.test(x)$p.value)
  
})

m<- r[1, ] # 平均値
par(mfrow=c(2, 1)) 

ttl1<- "正規母集団，標本平均（n=4）度数分布"
hist(m, freq=F, main=ttl1, col="gray", ylim=c(0, 1.5)) # 平均値の度数分布
curve(dnorm(x, mean=0, sd=1/sqrt(n)),
 add=T, col="red", lwd=2) # 正規曲線近似

ex<- expression(paste("正規分布，平均0，標準偏差", 1/sqrt(4)))
legend("topleft", ex, col="red", lw=2, bty="n")

p<- r[2, ] # 5%水準棄却数
length(p[p<=0.05])/k # 5%水準棄却率

ttl2<- "棄却率pの度数分布"
hist(p, freq=F, main=ttl2, col="gray") # 棄却 p 値の度数分布

結果として，標本平均の分布（図 1）を見ると，平均 0，標準偏差 1/sqrt(4) の正規分布となっていることがわかる。

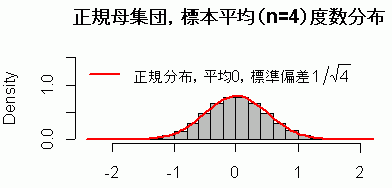
棄却率 p の度数分布を見ると（図 2），これまた予想通り，一様分布となる。

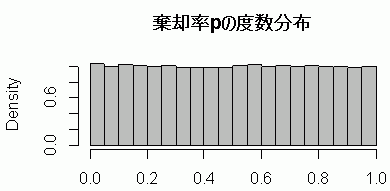
5％有意水準での棄却率は，0.04992 であり，水準どおりの棄却率であった。

以上のことは，正規母集団からの標本ならば，標本サイズが 4 であっても，理論的には t 検定で検定できることを示している。

3. t 検定のシミュレーション，母集団が非正規分布の場合，指数分布の例

非正規母集団から得られた標本に t 検定を適用した場合はどうなるだろうか？ここでは，よく知られた非負分布の一つであり，かつ，単純な式で表される指数分布を取り上げる。

指数分布は，一つの母数（パラメータ）で表され，それを λ とすると，確率密度関数 p(x) は次のようになる。

このとき，平均も標準偏差も 1/λ である。最も単純な λ = 1 の場合を考え，先ほどと同じく，以下のシミュレーションを行なってみよう。

1. 平均値 m の度数分布
2. 帰無仮説 H0: m = 0 に対して，5％有意水準で t 検定を行なったときの棄却率 p
3. 棄却率 pの度数分布

# 指数母集団からの標本（n=4）に対して t 検定

k<- 10000 # 標本取り出し反復回数
n<- 4 # 標本サイズ

r<- replicate(k, {

 x<- rexp(n, rate=1)
 c(mean(x), t.test(x)$p.value)
  
})

m<- r[1, ] # 平均値
par(mfrow=c(2, 1)) 

ttl1<- "指数母集団，標本平均（n=4）度数分布"
hist(m, freq=F, main=ttl1, col="gray", ylim=c(0, 1.5)) # 平均値の度数分布
curve(dnorm(x, mean=1, sd=1/sqrt(n)),
 add=T, col="red", lwd=2) # 正規曲線近似

ex<- expression(paste("正規分布，平均1，標準偏差", 1/sqrt(4)))
legend("topleft", ex, col="red", lw=2, bty="n")

p<- r[2, ] # 5%水準棄却数
length(p[p<=0.05])/k # 5%水準棄却率

ttl2<- "棄却率pの度数分布"
hist(p, freq=F, main=ttl2, col="gray") # 棄却p値の度数分布

標本平均の分布を見ると（図 3），平均 1，標準偏差 1/sqrt(4) の正規分布を想定した場合より，左に偏った分布となっている。

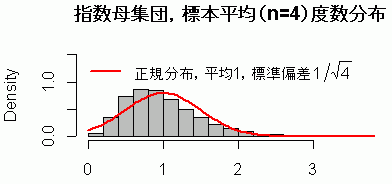
棄却率 p の度数分布を見ると，やはり左に偏った，つまり，小さい p 値が出やすい分布となっている。

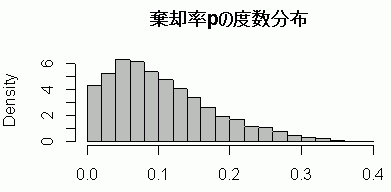
5％有意水準での棄却率は 0.2496，つまり，実際には 25％も棄却してしまう結果を生む。つまり，このような非正規母集団からの標本には t 検定は適用できないのである。 既に述べたように，母集団が正規分布でなくても，中心極限定理 によって，標本サイズが大きくなるにつれて，その平均値の分布は漸近的に正規分布に従うと見なせる。では，正規母集団と指数母集団から，大きさを変えて標本を抽出し，それを先ほどと同じく5%水準で t 検定してみよう。標本の大きさを， n = 2, 10, 30, 50, 100, 200 に設定した。

# 正規分布と指数分布，標本サイズによるt検定の違い

k<- 100000 # 標本取り出し反復回数
r1<- as.numeric(NULL)
r2<- as.numeric(NULL)

for (i in 1: 6) {

 switch(i, 
   n<- 2,
   n<- 10,
   n<- 30,
   n<- 50,
   n<- 100,
   n<- 200
  )

p<- replicate(k, {

 x1<- rnorm(n, mean=1, sd=1)
 x2<- rexp(n, rate=1)
 
 c(t.test(x1, mu=1)$p.value,
   t.test(x2, mu=1)$p.value)
  
})

r1[i]<- length(p[1, ][p[1, ]<=0.05])/k # 正規母集団の標本 棄却率
r2[i]<- length(p[2, ][p[2, ]<=0.05])/k # 指数母集団の標本 棄却率

}

x<- c(2, 10, 30, 50, 100, 200)

ttl<- "正規および指数母集団の標本 t 検定"
plot(x, r2, main=ttl, type = "b",
   ylim=c(0, 0.1),  yaxp=c(0, 0.1, 2), col="blue", pch=17,
   xlab="標本サイズ n", ylab="5%有意水準の棄却率") # 指数母集団の標本 棄却率変化

lines(x, r1, type = "b", col="red", pch=16) # 正規母集団の標本 棄却率変化

legend("topright", c("指数分布", "正規分布"),
    col=c("blue", "red"), pch=c(17, 16), lw=2, bty="n")

結果は，次の図 5 のようになった。

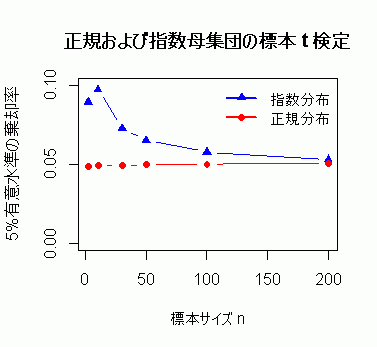
正規母集団の場合は，「統計学が最強の学問である（実践編）」が t 検定の適用が無理であるかのように述べた n = 4 どころか，理論的には n ≥ 2 ならば， t 検定は適用可能なのである。一方で，指数母集団の場合は，適切な結果を得るには，標本サイズが100以上必要だと言えよう。そのくらいの大きさの標本になると，中心極限定理によって， t 検定を適用しても良いだろうと考えられるのである。

Gosset の論文が，正規母集団を仮定した小標本 t 検定であるのは，まさに，このような理由によるものである。その論文を読むと， Introduction には以下のように書かれている。 “not strictly applicable to populations known not to be normally distributed” と書かれ，母集団（population）の非正規性には気を使っている様子が伺える。そして，最後の Conclusions でも，まず第一に “samples drawn from a normal population” に対する分布が発見されたことを述べ，その上で， “the curve represents the facts fairly well even when the distribution of the population is not strictly normal.” 厳密に母集団が正規分布でなくても，かなり良く適合するだろうと述べている。ところが，実際には，非正規分布の小標本の場合， t 検定は不適切と言えるのである。

4. t 検定の代わりに一般化線形モデルを使う，指数分布の例

では，非正規母集団の場合，どうしたら良いのだろうか？このように問いかけると，「ノンパラメトリック検定」，という答えがしばしば返ってくる。しかしながら，もし正規分布以外の何らかの確率分布が想定されるならば，それに基づいて一般化線形モデル（Generalized Linear Model, GLM）をまず検討すべきだろう。ここでは，前述の指数分布データ例に対して， t 検定と GLM を使って検定した結果を比較して見る。指数分布はガンマ分布の特殊形なので，ガンマ分布を想定すれば良い。

# 指数分布，標本サイズによるt検定とGLMの違い

k<- 100000 # 標本取り出し反復回数
r1<- as.numeric(NULL)
r2<- as.numeric(NULL)

for (i in 1: 6) {

 switch(i, 
   n<- 2,
   n<- 10,
   n<- 30,
   n<- 50,
   n<- 100,
   n<- 200
  )

p<- replicate(k, {

 x<- rexp(n, rate=1)
 
 c(t.test(x, mu=1)$p.value,
   summary(glm(x ~ offset(rep(1, n)), family = Gamma))$coefficients[4])
  
})

r1[i]<- length(p[1, ][p[1, ]<=0.05])/k # t検定 棄却率
r2[i]<- length(p[2, ][p[2, ]<=0.05])/k # GLM 棄却率

}

x<- c(2, 10, 30, 50, 100, 200)

ttl<- "指数母集団の標本 t 検定と GLM"
plot(x, r1, main=ttl, type = "b",
   ylim=c(0, 0.1),  yaxp=c(0, 0.1, 2), col="blue", pch=17,
   xlab="標本サイズ n", ylab="5%有意水準の棄却率") # 正規母集団の標本 t 検定 棄却率変化
lines(x, r2, type = "b", col="red", pch=16) # 指数母集団の標本 GLM 棄却率変化

legend("topright", c("t 検定", "GLM（ガンマ分布）"),
    col=c("blue", "red"), pch=c(17, 16), lw=2, bty="n")

結果は，次の図 6 のようになった。

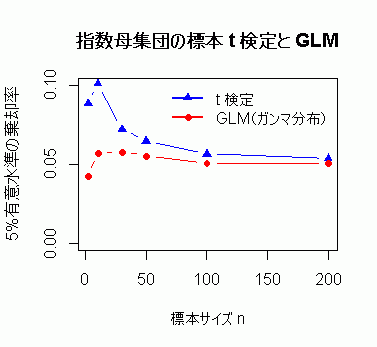
当然と言えば，当然なのだが，ガンマ分布に基づく GLM のほうが，標本サイズが小さくても，正しく棄却できることが分かる。

2018年に，嶋崎義浩さん（愛知学院大学歯学部）から，歯の数と医療費および入院日数との関係の分析の相談を受けたとき， Tweedie 分布に基づく GLM を推奨し，それによる分析が論文となった。

Saito, M., Shimazaki, Y., Nonoyama, T., & Tadokoro, Y. (2019)
Associations of number of teeth with medical costs and hospitalization duration in an older Japanese population
Geriatrics & Gerontology International 19(4): 335-341.

パソコンやソフトが発達した現代では，正規分布でなければノンパラメトリック検定という単純な発想は改めて，この論文のように，何か他の確率分布に従うのではないか検討してみるべきである。

5. 注意事項

通常の研究では帰無仮説が棄却されることが目的となっている。この場合，懸念されるのは，小標本に t 検定を適用し，棄却されたから，それで良し，という研究が，無意識に，あるいは，もしかして意図的に出ているのではないか，という点である。いずれにしても，小標本の検定は，著者も，読者も，十分注意する必要がある。

関連ページ

• 信頼区間がマイナスになる場合: 平均と比率
• 対応のある t 検定から線形混合モデルへ
• 反復測定の比率データ: 一般化線形混合モデル ロジスティック回帰
• 母比率の差の信頼区間と多重比較: 季節性胃潰瘍について
• ポアソン分布 2 群検定と t 検定 U 検定との比較: Q-Q plot も利用