信頼区間がマイナスになる場合: 平均と比率
井口豊(生物科学研究所,長野県岡谷市)
最終更新: 2022 年 12 月 6 日
1. はじめに
信頼区間の下限が負(マイナス)になるのは,信頼区間の算出に適した母集団を想定していない場合がある。ここでは,母比率と母平均の 95 % 信頼区間を統計ソフト R で計算した場合を紹介する。
2. 母比率の信頼区間
母比率の信頼区間の計算では,ド・モアブル-ラプラスの定理に基づいて,標本比率が正規分布に従う,と考えて計算することがある。そのため信頼区間が負になる場合が出てくる。
この場合は,正確な信頼区間として,二項分布を使い計算する。もちろん,負にならなくても,最初から二項分布の信頼区間として計算するほうが良い。
便宜上,極端な例ではあるが, 9 人を検査して, 1 人が陽性だった場合の陽性母比率の信頼区間を計算する。
#############
# データ
n<- 9
pos<- 1
# 陽性率
p<- pos/n
# 正規近似の信頼区間
zs<- 1.96 * sqrt(p*(1 - p)/n)
approx.ci.1<- p - zs
approx.ci.2<- p + zs
# 二項分布の信頼区間
exact.ci.1<- binom.test(pos, n)$conf.int[1]
exact.ci.2<- binom.test(pos, n)$conf.int[2]
# データフレーム
g.df<- data.frame(
Confidence.interval = factor(c("Normal.approx", "Binomial")),
Positive.ratio = c(p, p),
CI.low = c(approx.ci.1, exact.ci.1),
CI.up = c(approx.ci.2, exact.ci.2)
)
head(g.df)
# グラフ
library(ggplot2)
g<- ggplot(
g.df,
aes(
x = Confidence.interval, y = Positive.ratio
)
) +
geom_hline(
yintercept = 0, linetype = "dashed"
) +
geom_errorbar(
aes(ymin = CI.low, ymax = CI.up),
width = 0.1) +
geom_point(size = 2) +
ylim(- 0.2, 0.6) +
theme_classic() +
ggtitle(
"Positive.ratio \n with 95% CI"
)
plot(g)
################
結果は,次の図 1 のとおりである。
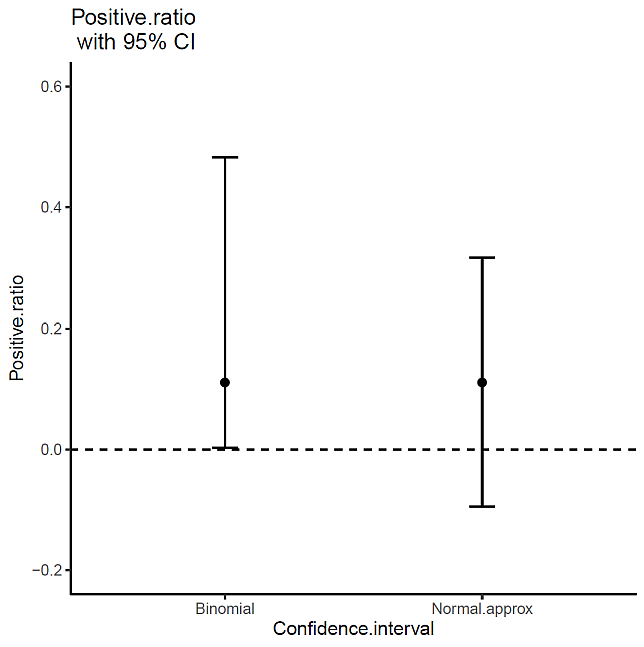
二項分布を利用して,正確な信頼区間を求めると,負にならず,さらに,上限も過小評価しない。
3. 母平均の信頼区間
様々な検査値には,正常値は,ほぼゼロ(検出限界以下)だが,異常になると,大きな値が出てくるものがある。
そのような場合も,正規分布を前提として信頼区間を求めると,下限が負になる場合がある。
このとき,すぐに,中央値とか,四分位数とかが思い浮かぶのだが,まずは,何らかの確率分布に従っていないか,それを調べるべきである。
例えば,以下のデータに対して,通常の線形モデルで正規分布の場合と,一般化線形モデル(Generalized Linear Model, GLM)でガンマ分布の場合を適用し, Q-Q プロットで調べてみた。
#############
# データ
x<- c(
0.70, 0.05, 0.10, 0.05, 4.20,
0.20, 2.20, 0.05, 3.10, 6.00,
0.05, 0.20, 0.05, 0.10, 14.30,
1.20, 0.05, 0.10, 0.05, 0.05,
0.50, 8.80, 1.60, 0.10, 0.05,
0.05, 0.10, 0.90, 40.10, 0.30
)
# 線形モデル 正規分布
mod.norm<- lm(
x ~ 1
)
# 一般化線形モデル ガンマ分布
mod.gamma<- glm(
x ~ 1,
family = Gamma(link ="identity")
)
# Q-Q プロット
library(DHARMa)
par(mfrow = c(2, 1))
plotQQunif(
mod.norm, testOutliers=F, testDispersion=F
)
plotQQunif(
mod.gamma, testOutliers=F, testDispersion=F
)
################
結果は,次の図 2 のとおりである。
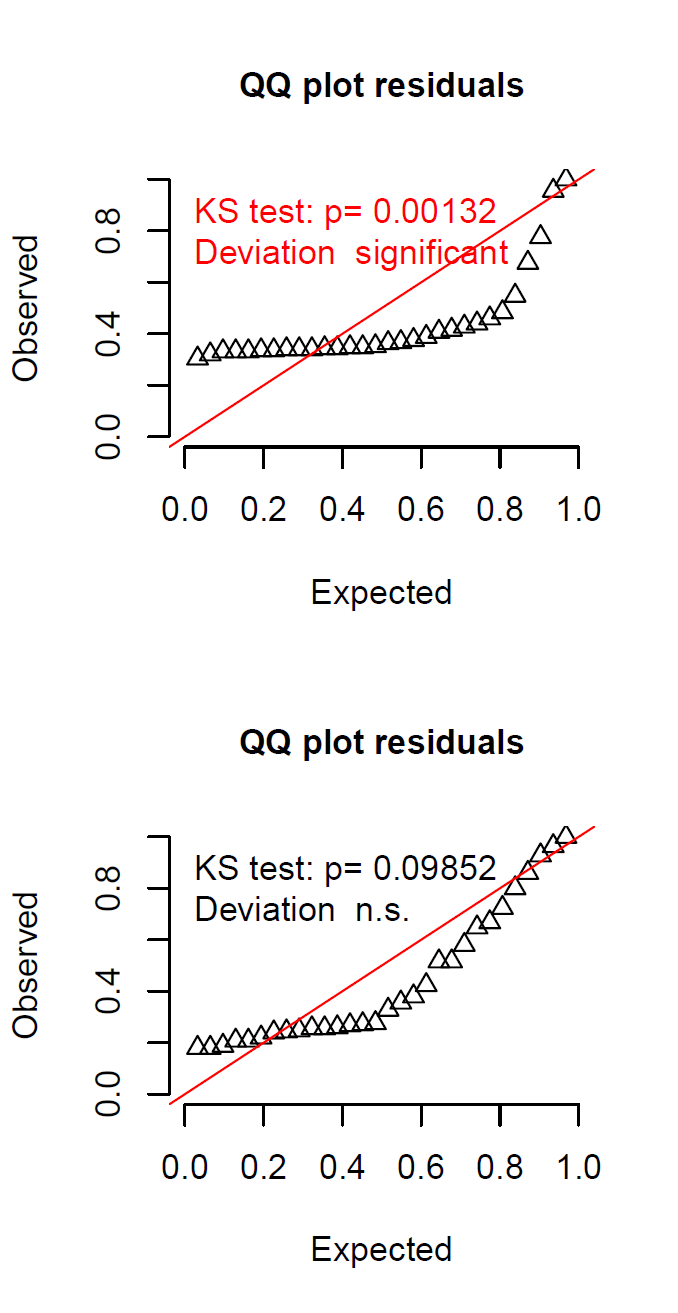
このデータは,線型モデルの正規分布よりも,一般化線形モデルのガンマ分布に適合していると想定された。
実際に,両方のモデルでの信頼区間を求めて見よう。
#############
# 線形モデル 正規分布 信頼区間
mod.norm<- lm(
x ~ 1
)
norm.ci.1<- confint(mod.norm)[1]
norm.ci.2<- confint(mod.norm)[2]
# 一般化線形モデル ガンマ分布 信頼区間
mod.gamma<- glm(
x ~ 1,
family = Gamma(link ="identity")
)
gamma.ci.1<- confint(mod.gamma)[1]
gamma.ci.2<- confint(mod.gamma)[2]
# データフレーム
g.df<- data.frame(
Confidence.interval = factor(c("Normal", "Gamma")),
Mean = c(mean(x), mean(x)),
CI.low = c(norm.ci.1, gamma.ci.1),
CI.up = c(norm.ci.2, gamma.ci.2)
)
s.df<- data.frame(
Confidence.interval = factor(
rep(c("Normal", "Gamma"), each = length(x))
),
Measurement = c(x, x)
)
head(g.df)
head(s.df)
# グラフ
library(ggplot2)
library(ggbeeswarm)
g<- ggplot(
s.df,
aes(
x = Confidence.interval, y = Measurement
)
) +
geom_beeswarm() +
geom_point(
data = g.df,
aes(x = Confidence.interval, y = Mean),
size = 3, color="red"
) +
geom_hline(
yintercept = 0, linetype = "dashed"
) +
ylim(- 1, 45) +
geom_errorbar(
data = g.df,
aes(
x = Confidence.interval, y = Mean,
ymin = CI.low, ymax = CI.up),
size = 1, width = 0.1, color="red"
) +
theme_classic() +
ggtitle(
"Mean \n with 95% CI"
)
plot(g)
################
結果は,次の図 3 のとおりである。
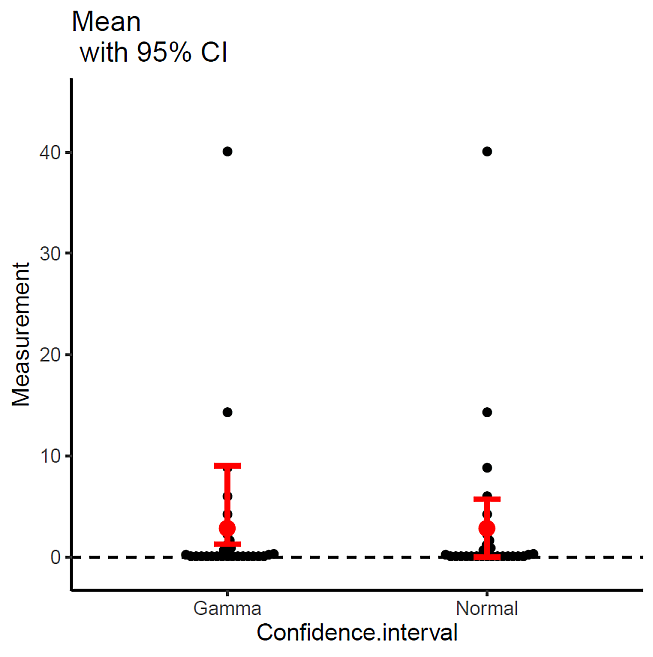
グラフでは分かりづらいが,正規分布の場合,信頼区間下限が負になっている。しかし,ガンマ分布を利用して信頼区間を求めると,負にならず,上限も正規分布の場合よりも上になる。
さらに,正規分布の場合は,平均を挟んで信頼区間が上下対称だが,ガンマ分布の場合は,上に伸びた区間となっている。
たとえ信頼区間が負にならなくても,正規分布が想定されないデータには,一般化線形モデルを考えてみるべきである。
なお,誤解が多いが,正規分布に従うかどうかと,パラメトリック検定を適用するかどうかは,必ずしも関係ない。上記の例は,正規分布は仮定できないが,ガンマ分布を仮定したパラメトリック検定である。