対応のある t 検定から線形混合モデルへ

井口豊（生物科学研究所，長野県岡谷市）
最終更新：2024 年 1 月 15 日

1. はじめに

対応のあるデータ（paired data）に対して，対応のある t 検定（paired t test）を適用するのは，ごく一般的なことである。ここでは，対応するデータの相関の強弱によって，有意差の検出率がどのように変わるか，対応のある t 検定と線形混合モデル（linear mixed model）によって調べてみた。

なお，相関の強弱の基準については，「慣習として」などと漠然と教えられることが多々あるので，別ページに詳しく解説した（統計学の基準値の由来：5%有意水準，カイ二乗検定，相関係数の出典と引用）。

2. データ

対応する標本の大きさを 10 （sample size, n = 10），平均をそれぞれ 10，11，標準偏差を共に 1，Pearson 相関の母相関係数 r が 0 から 0.6 となる 1000 個の乱数を発生させて，対応のある t 検定と線形混合モデルの検定を行ない，有意水準 5% で棄却される比率を統計解析ソフト R を用いてシミュレーションで調べた。

2. R スクリプト

##########
library(MASS)
library(blme)
library(parameters)

m<- c(10, 11) # 対応データの各平均
n<- 10  # 標本サイズ
k<- 10000 # 標本抽出回数

sub<- factor(rep(1:n, 2))
time<- rep(1:2, each=n)

p.lmm<- as.numeric(NULL)
p.tpair<- as.numeric(NULL)

for(i in 1:5) { 

r<- (i-1)*0.2
sig<- matrix(c(1, r, r, 1), ncol=2)

p<- replicate(k, {

 dat<- mvrnorm(n=n, mu=m, Sigma=sig)
 y<- c(dat[, 1], dat[, 2])

 p1<- p_value(blmer(y ~ time + (1|sub),
    control=lmerControl(calc.derivs=F)))$p[2]
 p2<- t.test(y ~ time, paired=T)$p.value

 c(p1, p2)
})

p.lmm[i]<- length(p[1, ][p[1, ]<0.05])/k
p.tpair[i]<- length(p[2, ][p[2, ]<0.05])/k
}

p.lmm # 線形混合モデルによる棄却率
p.tpair # 対応あるt検定による棄却率

# グラフ
x<- seq(0, 0.8, by=0.2)
plot(x, p.lmm,
 ylim=c(0.5, 1), col="red", pch=16, type="o",
 xlab="Correlation coefficient r", ylab="Rejection rate"
)

lines(x, p.tpair,
 ylim=c(0.5, 0.1), col="blue", pch=16, type="o"
)

legend("topleft", legend=c("LMM", "t test"),
 col=c("red", "blue"),
 pch=16, lty=1
)

##############

3. 結果と考察

シミュレーション結果の一例のグラフは，次のようになる。

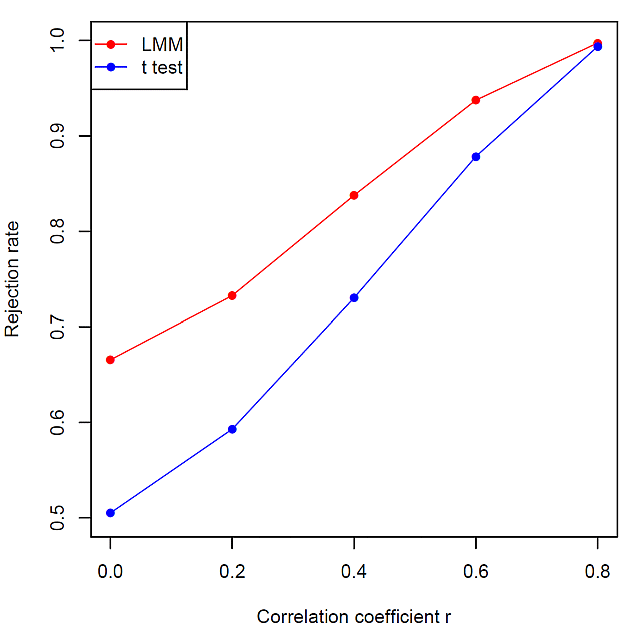
当然と言えば，当然なのだが，対応するデータの相関が強くなるほど棄却率が上がり，有意差の検出力が高くなる。だからこそ，対応のあるデータに，独立 2 標本 t 検定でなく，対応のある t 検定が適用される。しかしながら，t 検定における，この「対応あり」「対応なし」の使い分け理由が，教えられないことが多々ある。

一方，対応のある t 検定と線形混合モデルの検出力を比べると，線形混合モデルのほうが全体的に高くなり，相関が弱いほど，その違いが顕著となる。

大学などでは，t 検定を教えることがあっても，線形混合モデルまで教えることなく，授業を終えることが多いようだ。せっかくパソコンの性能が向上し，フリーソフト R で簡単に計算できるのだから，授業の中でも，多少なりとも，線形混合モデルについて触れてほしいものである。

私自身としては，使えるものは使え，という信条で，混合モデルの利用を薦めている。私が共著でもある教育心理学的研究でも，線形混合モデルが使われた。

尾之上高哉・井口豊 (2020)
ブロック練習と交互練習の単独効果と複合効果の比較検討
—学習内容の定着度，及び，確信度判断の正確性に着目して—
教育心理学研究 68(2): 122-133.

尾之上高哉・井口豊・丸野俊一 (2017)
目標設定と成績のグラフ化が計算スキルの流暢性の形成に及ぼす効果
—小学3・4年生を対象とした学級規模での指導を通して—
教育心理学研究 65(1): 132-144.

さらに，高校生の卒論の統計データ解析を指導したときも，一般化線形混合モデルを使ってもらった（高校卒論「目立つ書体の組み合わせとは」一般化線形混合モデルを使って）。

高校生でさえ，混合モデルで分析できる時代なのである。大学授業では，それが一般的に扱われて当然だろう。。