logo
生物科学研究所 井口研究室
Laboratory of Biology, Okaya, Nagano, Japan
Home

t 検定の正規性も残差を調べる：検定の多重性問題

井口豊（生物科学研究所，長野県岡谷市）
最終更新： 2022 年 12 月 31 日

1. はじめに

2 群の母平均の差の検定である t 検定の正規性を調べるのに， 2 群別々に検定して，異なる判断結果に出会ってしまい，困っている学生を見かけたことがある。学生に限らず，研究者でも，そういう事例がありそうだ。

このサイトの表題に，t 検定の正規性も，と書いたのは，以前，分散分析で同様な問題を扱ったからである。

t 検定は，分散分析で 2 群の平均の差を検定する方法であることも既に述べた。

したがって， t 検定の正規性も残差分析すれば良いのだが，これもあまり知られていない感じである。 GraphPad の統計ソフト Prism の解説を読むと，その状況は日本だけでもないらしい。 Residuals tab: t tests の冒頭に以下のように書かれている。

Many scientists think of residuals as values that are obtained with regression. But the t test is really regression in disguise.

この説明で regression in disguise という表現が，何とも面白い。裏を返せば， t 検定も回帰（分析）なのだが，それに気づかない科学者も多い，ということだろう。

ここでは R を利用して，まず t 検定の残差の正規性を調べる二つの方法を取り上げる。

その上で，群ごとの正規性検定の問題点を説明した

さらに後半では，別のタイプの t 検定の正規性も説明した。

いずれも，統計ソフト R を利用している。

2. 群データの中心化によって残差正規性を調べる

t 検定の残差の正規性を調べる基本的方法が，前述の Prism の解説 Residuals tab: t tests にも書かれているように，それぞれの群のデータを中心化（センタリング centering）して， 2 群のデータをまとめて正規性を調べる方法である。

要するに，それぞれの群で，各データから群平均を引いて（減じて），その変換されたデータを両群で一緒にして，正規性を調べるのである。中心化は， R の scale 関数で，分散を変えない設定でも可能である。

以下のような大きさ 20 (n = 20) の標本 A, B で，独立（対応のない） 2 群の t 検定の残差の正規性を， Shapiro-Wilk 正規性検定と Q-Q プロットで調べてみる。 


#############
# データ
A<- c(
  43, 42, 47, 35, 49, 42, 34, 36, 40, 40, 
  31, 43, 38, 41, 42, 46, 43, 44, 37, 38
)

B<- c(
  62, 60, 56, 55, 59, 63, 61, 56, 57, 57,
  53, 58, 60, 64, 67, 60, 67, 60, 66, 66
)

# 定義式による中心化とデータの統合
A1<- A - mean(A)
B1<- B - mean(B)

y1<- c(A1, B1)

# scale 関数による中心化とデータの統合
A2<- scale(A, scale = F)
B2<- scale(B, scale = F)

y2<- c(A2, B2)

# 2 種類の中心化法の比較（同じ結果）
cbind(y1, y2)

# データ y1 利用（y2 も可）
# Shapiro-Wilk 正規性検定
shapiro.test(y1)

# 正規 Q-Q プロット
qqnorm(y1)
qqline(y1, col=2)
 
################

Shapiro-Wilk 正規性検定の結果は，
p-value = 0.8551
であり， Q-Q プロットは，次の図 1 のようになった。

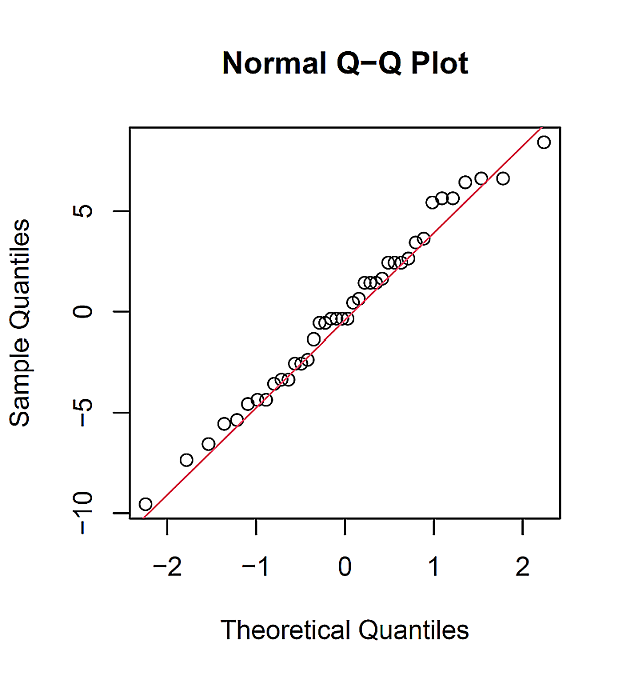
t 検定の残差の Q-Q プロット

図 1. t 検定の残差の Q-Q プロット

3. ダミー利用の線型回帰によって残差正規性を調べる

最初に述べたとおり， t 検定は回帰分析と同等であり，同じ線型モデル（linera model）に属する。したがって， R ならば，線型モデル関数 lm を利用して，残差の正規性を調べることができる。

前述の標本 A, B の数値を目的変数 y とし， A, B それぞれに，ダミー変数 x として 0, 1 を割り当て説明変数として，回帰分析を行い，その残差の正規性を， Shapiro-Wilk 正規性検定と Q-Q プロットで調べてみる。 


###################
# A, B をダミー変数 0, 1 の説明変数 x とする。
x<- rep(0:1, c(length(A), length(B)))

# A, B の数値データをまとめて，目的変数 y とする。
y<- c(A, B)

# 線型回帰モデル
mod<- lm(y ~ x)

# 回帰残差
resid<- mod$residuals

# Shapiro-Wilk 正規性検定
shapiro.test(resid)

# 正規 Q-Q プロット
qqnorm(resid)
qqline(resid, col=2)

################

結果は省略するが， Shapiro-Wilk 正規性検定も，正規 Q-Q プロットも，先ほどと全く同じ結果となる。

次に，この回帰分析の結果をグラフ化して， A, B の平均の位置も図示する。 


##################
# x, y データフレーム
df<- data.frame(x, y)

# サンプル名を付ける
df$sample<- rep(c("A", "B"), c(length(A), length(B)))

# A, B の平均
df.mean<- data.frame(
    Mean = c(mean(A), mean(B)),
    sample = c("A", "B")
)

# グラフ内の注釈
t.lab = c("Mean A", "Regression line", "Mean B")
x.lab = c(0.5, 0.3, 0.5)
y.lab = c(
   mean(A) + 2, (mean(A) + mean(B))/2 + 2, mean(B) + 2
)

# グラフ
library(ggplot2)

g<- ggplot(df, aes(x = x, y = y)) +
   geom_point(aes(color = sample, shape = sample), size = 3)+
   theme_classic()+ theme(text = element_text(size = 14)) +
   geom_smooth(method="lm",se = FALSE, fullrange = FALSE) +
   geom_hline(
       data = df.mean, 
       aes(yintercept = Mean, color = sample),
       linetype = "dashed", size = 1.2
      ) +
   annotate(
    "text", label = t.lab,
      x = x.lab, y = y.lab, size = 5)

g

################

結果は以下の図 2 のようになり， A と B の平均の差が，回帰直線の傾きに相当し， t 検定がダミー変数を用いた回帰分析であることが分かる。

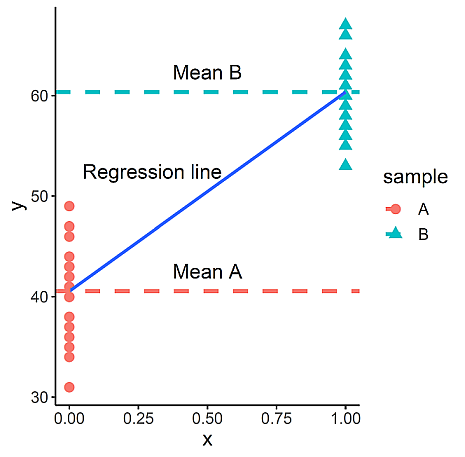
回帰直線と平均の差

図 2. 回帰直線と 2 群の平均の差

4. 2 群別々に正規性検定することの問題点

2 群別々に正規性検定すると，何が問題なのか？これは，検定の多重性の問題が生じるのである。このことは，分散分析のケースで述べた。

t 検定でも，これは同様である。

ここでは，両群とも大きさ 10 の標本として，この標本を標準正規母集団から 10 万回繰り返し取り出すシミュレーションをおこなってみる。

その上で， Shapiro-Wilk 正規性検定をおこない，いずれかの群が， 5 ％水準 (α = 0.05) で棄却される比率を調べる。すなわち，第一種過誤率 (Type I error rate) を調べる。同様にして，分散分析残差のShapiro-Wilk 正規性検定による棄却率も調べて，両者の結果を比較する。

さらに今回は，両群を別々に正規性検定し，それに Bonferroni 補正した結果も加えた。

以下が， R スクリプトである。 


#############

np <- npbon<- npres<- 0

k <- 1e+5
n<- 10

for (i in 1:k) {  

# 2 群データ
  A<- rnorm(n)
  B<- rnorm(n)

# 2 群の統合データ
  dat<- c(A, B)

# 群ダミー
  group<- rep(0:1, each = n)

 # 線型モデル残差
  resid<- lm(dat ~ group)$residuals

  # 群ごとの正規性検定
  p.A<- shapiro.test(A)$p.value
  p.B<- shapiro.test(B)$p.value

  if (p.A < 0.05 || p.B < 0.05) {
   np <- np + 1
  }

  # 群ごとの正規性検定 Bonferroni 補正
  if (p.A < 0.025 || p.B < 0.025) {
   npbon <- npbon + 1
  }

  # 残差の正規性検定
  p.res<- shapiro.test(resid)$p.value

  if (p.res < 0.05) {
   npres <- npres + 1
  }
}

# 5% 水準での棄却率
# 群別の正規性検定
npr <- np/k

# 群別の正規性検定 Bonferroni 補正
npbonr <- npbon/k

# 残差の正規性検定
npresr <- npres/k

barplot(
 c(npr, npbonr, npresr), 
 ylim = c(0, 0.2), col = "#0080ff",
 main = "Normality test for t test",
 names.arg =c(
      "Each group",
      "After correction",
      "Residuals"
      ),
 ylab = "Type I error rates with alpha level 0.05"
)
abline(h = 0.05, col = "red", lwd = 2)

################

結果は，次の図 3 のとおりである。

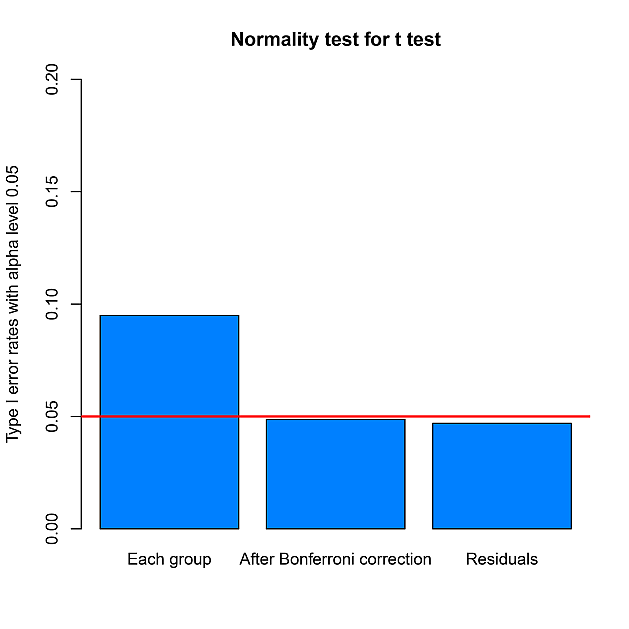
t 検定 3 種類の正規性検定

図 3. 独立 2 群（対応ない） t 検定の群ごと正規性検定（左），その Bonferroni 補正（中），および，残差の正規性検定（右）の 5 ％水準棄却率

群ごとに正規性検定すると，正しく棄却されないことが一目瞭然である。 正規分布を有意水準以上に棄却してしまうのである。

したがって，ダミー変数利用の線型モデル，または，群データをセンタリングして全体の残差正規性を調べれば良いのだが，それを理解していないような人も多い。

5. Welch 検定の正規性

ただし，全体の残差正規性の検定で困るのは， Welch 検定を行う場合である。この場合は，群ごとで Bonferroni 補正して検定することになる。最近では，等分散検定せずに， Welch 検定を行うことが標準的な手順となりつつある。これも検定の多重性を回避するためである。

t 検定の正規性検定でも，正規性検定すること自体が，同様な検定の多重性の問題を生ずる。

したがって，正規性検定自体を行わず，ヒストグラムや Q-Q プロットでの確認にとどめる，という手順が推奨されても良い。

6. 対応ある t 検定の正規性

対応ある t 検定は，実質的に 2 群の検定ではなく，対応するデータの差の 1 群検定である。

したがって，その正規性も，対応するデータの差を取って，その検定をする。前述の Prism の解説 Residuals tab: t tests にも同様に書かれている。

関連サイト

Home