分散分析の正規性は残差を調べる:検定の多重性問題
井口豊(生物科学研究所,長野県岡谷市)
最終更新: 2022 年 9 月 12 日
1. はじめに
分散分析 ANOVA は多群や多要因の母平均の差の検定であるが,その正規性に関して,どこを調べれば良いのか,日本語の解説は少ない。そのためなのか,群ごとや,要因の水準ごとに正規性を検定するものと思っている人も多いようだ。ここでは,そのとき生じる問題について解説する。
実は,分散分析の正規性検定ついては,統計ソフトの使い方として解説されているものも少なくない。
例えば, Minitab 応答は正規分布に従う必要があるか,
分散分析モデルの残差が正規分布に従うと仮定します
,
と説明されている。
あるいは, jamovi ANOVA(分散分析),
分散分析は残差(誤差)が正規分布であり
,
と説明されている。
さらに, R を利用した STHDA (Statistical tools for high-throughput data analysis) の Two-Way ANOVA Test in R, そのページの Check the normality assumpttion,
The normal probability plot of residuals is used to verify the assumption that the residuals are normally distributed
と説明され,残差の Q-Q プロットが示されている。
要するに,多要因,多群の分散分析の正規性は,その残差の正規性を調べれば良いのだが,意外と知らない人が多いのである。
さらに, t 検定の正規性も残差分析するのだが,それは別ページに解説した。
2. 何が問題になるのか
では,群ごとや,要因の水準ごとに正規性を検定すると,何が問題なのか?ごく簡単なことで,検定の多重性が問題になるのである。
ここでは, 2 要因分散分析を例にして,要因の水準ごとに正規性検定した場合と,残差の正規性を検定した場合で,正規分布であるという帰無仮説の棄却率を比較してみる。
3. 要因の水準ごとの正規性検定と残差正規性の検定
モデルを単純化するために,2 要因, 2 水準で,どちらの要因も対応無し,という場合を考える。いわゆる 2 要因参加者間(ABs デザイン)である。各要因の水準は, A1B1, A1B2, A2B1, A2B2, いずれの水準も大きさ 10 の標本として,全体で n = 40 とする。
この標本を標準正規母集団から 10 万回繰り返し取り出すシミュレーションを行う。
その上で, Shapiro-Wilk 正規性検定をおこない,各要因の水準いずれかが, 5 %水準 (α = 0.05) で棄却される比率を調べる。すなわち,第一種過誤率 (Type I error rate) を調べる。同様にして,分散分析残差のShapiro-Wilk 正規性検定による棄却率も調べて,両者の結果を比較する。
以下が, R スクリプトである。
#############
np <- npres<- 0
k <- 100000
for (i in 1:k) {
y<- rnorm(40)
A<- factor(rep(1:2, each = 20))
B<- factor(rep(c(1:2, 1:2), each = 10))
data.frame(A, B, y)
# 分散分析
mod<- aov(y ~ A * B)
# 残差
resid<- mod$residuals
# 各要因の水準組み合わせの正規性検定
p.A1B1<- shapiro.test(y[1:10])$p.value
p.A1B2<- shapiro.test(y[11:20])$p.value
p.A2B1<- shapiro.test(y[21:30])$p.value
p.A2B2<- shapiro.test(y[31:40])$p.value
if (p.A1B1 < 0.05 || p.A1B2 < 0.05 ||
p.A2B1 < 0.05 || p.A2B2 < 0.05) {
np <- np + 1
}
# 残差の正規性検定
p.res<- shapiro.test(resid)$p.value
if (p.res < 0.05) {
npres <- npres + 1
}
}
# 5% 水準での棄却率
# 要因別の正規性検定
npr <- np/k
# 分散分析の残差検定
npresr <- npres/k
barplot(
c(npr, npresr), ylim = c(0, 0.2), col = "#0080ff",
main = "Normality test for ANOVA",
names.arg =c(
"Normality for each level",
"Normality for residuals"
),
ylab = "Type I error rates with alpha level 0.05"
)
abline(h = 0.05, col = "red", lwd = 2)
################
結果は,次の図 1 のとおりである。
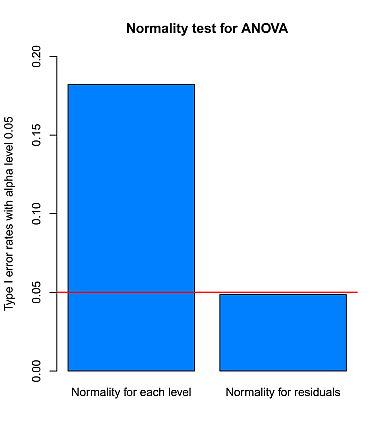
水準ごとに検定すると,正しく棄却されないことが一目瞭然である。 正規分布を有意水準以上に棄却してしまうのである。
逆に言えば,冒頭に述べたように,分散分析の残差正規性を調べれば良いのだが,どうも,このあたりを理解していないような人が多い感じである。