統計解析を用いた信頼性の評価 2. 医工学治療 30,倉持龍彦ほか(2018)
井口豊(生物科学研究所,長野県岡谷市)
最終更新:2018年11月17日
倉持龍彦・對馬栄輝・下井俊典・井口豊・宮田賢宏・大塚紹・大友学・若狭伸尚・村野勇・米津太志・角田恒和(2018)
統計解析を用いた信頼性の評価 2
医工学治療 30 (3): 149-155.
土浦協同病院の倉持龍彦さんから,待望の論文別刷りが届いた。信頼性の統計学的評価,その第二弾である。第一弾は,既に,別ページで紹介した(統計解析を用いた信頼性の評価1. 医工学治療 30,倉持龍彦ほか(2018))。
これまた倉持さんだからこそできた労作である。私も協力でき,かつ,共著になることができ,光栄である。
まず特筆すべき点は, Bland-Altman plot について,なんと,4ページに及ぶ解説をしていることである。これだけでも,統計データ解析の授業の資料になりそうだ。
その後,通常回帰,主成分回帰, Deming 回帰,幾何平均回帰,Passing-Bablock 回帰を解説している。簡単に図示すると,以下のような計算である(同論文の図 5 を簡略化)。
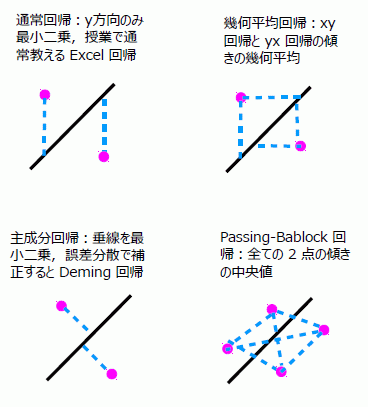
実は,大学などで教える回帰は,通常回帰だけ,というのが現状なのである。しかも,この回帰が y 方向の最小二乗しか考慮していない点を知らない(学んでも忘れている?)人が非常に多い。大学教員ですら理解せずに,「回帰分析」を使っている人がいるのである。
倉持さんには,大学や病院関係などで,講演して欲しいと思っている。
ここに挙げた回帰の中で,ホタルの体サイズの規則性を調べるために私が使ったのは,主成分回帰だった。
井口豊 (2007)
ゲンジボタルとヘイケボタルにレンシュの法則はあてはまるか?
全国ホタル研究会誌 40: 32-34.