logo
生物科学研究所 井口研究室
Laboratory of Biology, Okaya, Nagano, Japan
Home

効果量 偏イータ二乗と一般化イータ二乗を比較: 反復測定分散分析

井口豊（生物科学研究所，長野県岡谷市）
最終更新： 2022 年 11 月 20 日

1. はじめに

反復測定分散分析の効果量として，偏イータ二乗（partial η2）と一般化イータ二乗（generalized ηG2）を比較した。

統計ソフト R を利用して，二元配置分散分析で， 1 要因に対応あり， 1 要因に対応なし，いわゆる混合計画モデルで， 2 群，標本サイズ各 10 の 2 反復するシミュレーションを行い，前述 2 種の効果量を比較し，その関連性を調べた。

一般化イータ二乗の効果量として， Bakeman (2005) が推奨した基準で，その大中小を比べた。シミュレーションで示したのは，反復要因（対応ある要因）の主効果である。文献の詳細は，ページ最後に一括して挙げた。

2. 偏イータ二乗と一般化イータ二乗の比較シミュレーション 


###########################
# 効果量パッケージ
library(DescTools)

# 反復測定分散分析シミュレーション


p<- replicate(5000, {

m<- runif(n = 4, 0, 3)

dat<- c(
  rnorm(10, mean = m[1]),
  rnorm(10, mean = m[2]),
  rnorm(10, mean = m[3]),
  rnorm(10, mean = m[4])
)

v1<- factor(rep(1:2, each = 20)) # between subjects
v2<- factor(rep(rep(1:2, each = 10), 2)) # within subjects
sub<- factor(c(rep(1:10, 2), rep(11:20, 2)))

mod<- aov(dat ~ v1 * v2 + Error(sub/(v2)))

es<- EtaSq(mod, type = 1, anova = TRUE)

 c(
  es[2, 2], # partial eta-squared 
  es[2, 3]  #  generalized eta-squared
 )
})

# 回帰式当てはめ
lm(p[1, ] ~ -1 + p[2, ] + I(p[2, ]^2))

# グラフ
library(ggplot2)

dat<- data.frame(
   Partial.eta.squared = p[1, ],
   Generalized.eta.squared = p[2, ]
)

df.1 <- data.frame(
  x = c(-0.2, 0.02, 0.02, -0.2, 0.13, 0.13, -0.2, 0.26, 0.26),
  y = c(0.04, 0.04, -0.2, 0.23, 0.23, -0.2, 0.42, 0.42, -0.2),
  Effect.size = factor(rep(c(
    "small", "medium", "large"), each = 3
   ))
)

t.lab = c("0.02", "0.13", "0.26", "0.04", "0.23", "0.42")
x.lab = c(0.05, 0.16, 0.29, -0.03, -0.03, -0.03)
y.lab = c(-0.03, -0.03, -0.03, 0.06, 0.25, 0.44)

g<- ggplot(dat, aes(
   Generalized.eta.squared, Partial.eta.squared)
   ) + 
  geom_point() + theme_classic() +
  theme(text = element_text(size = 14)) +
  coord_cartesian(xlim = c(-0.03, 0.6), ylim = c(-0.03, 0.6))
g + geom_line(dat = df.1,
  aes(x = x, y = y, color = Effect.size), size = 1.2) +
  theme(legend.position=c(0.8, 0.5), 
        legend.justification=c(1,1)) + 
  annotate(
    "text",label = t.lab,
      x = x.lab, y = y.lab, size = 5)

########################

結果は，以下の図 1 のようになった。

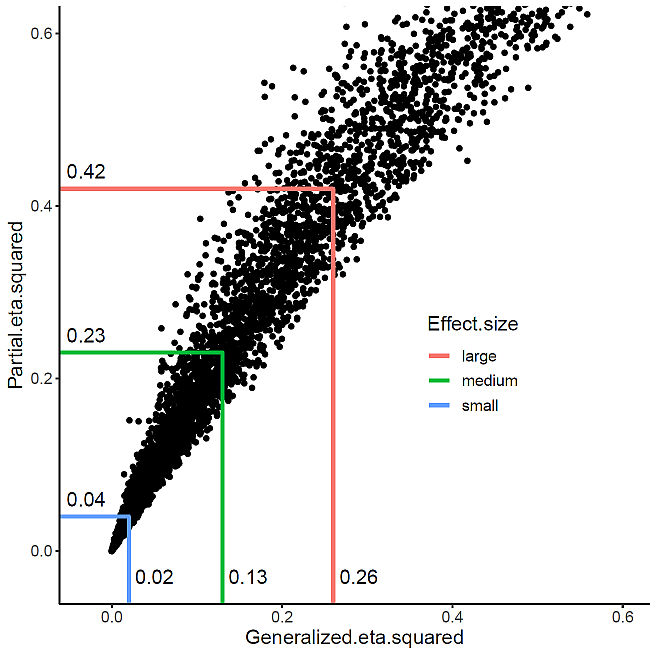
偏イータ二乗と一般化イータ二乗の関係

図 1. 偏イータ二乗と一般化イータ二乗の関係

効果量が大きくなるほど，両者の数値が乖離することが分かる。Bakeman (2005)による一般化イータ二乗の効果基準と比較して，その約 2 倍が偏イータ二乗に相当する。

3. 偏イータ二乗か，一般化イータ二乗か

Bakeman (2005) は，論文タイトルどおり，一般化イータ二乗を推奨しているが，それでもなお，研究デザインが変わらなければ，偏イータ二乗についても，その範囲内で独自の基準を設定することが出来る，と述べている（p.383 左段）。

反復測定分散分析に，どちらの効果量が良いかと，私も質問をされることがある。上記のグラフのように，両者には関連性があるので，その特徴を理解した上で，どちらでも使えば良い，と私は思う。

関連サイト

参考文献

Bakeman (2005) Recommended effect size statistics for repeated measures designs
Behavior research methods 37(3): 379-384.

Home