生物科学研究所 井口研究室
Laboratory of Biology, Okaya, Nagano, Japan
効果量イータ二乗と偏イータ二乗を比較: 二元配置分散分析
井口豊(生物科学研究所,長野県岡谷市)
最終更新: 2022 年 11 月 20 日
1. はじめに
二元配置分散分析の効果量として,イータ二乗(η2)と偏イータ二乗(partial η2)を比較した。
統計ソフト R を利用して,対応の無いデータの二元配置分散分析,各 3 水準,標本サイズ各 10 のシミュレーションを行い,前述 2 種の効果量を比較し,その関連性を調べた。
なお,シミュレーションしたのは,一つの要因の主効果である。
2. イータ二乗と偏イータ二乗の比較シミュレーション
###########################
# 効果量パッケージ
library(DescTools)
# 二元配置分散分析シミュレーション
p<- replicate(5000, {
m<- runif(n = 3, 0, 3)
dat<- c(
rnorm(10, mean = m[1]),
rnorm(10, mean = m[2]),
rnorm(10, mean = m[3])
)
v1<- factor(rep(1:3, each = 10))
v2<- factor(rep(1:3, 10))
mod<- aov(dat ~ v1 * v2 )
es<- EtaSq(mod)
c(
es[1, 1], # eta-squared
es[1, 2] # partial eta-squared
)
})
# 回帰式当てはめ
lm(p[2, ] ~ p[1, ] -1)
# グラフ
library(ggplot2)
dat<- data.frame(
Eta.squared = p[1, ],
Partial.eta.squared = p[2, ]
)
df.1 <- data.frame(
x = c(-0.2, 0.01, 0.01, -0.2, 0.06, 0.06, -0.2, 0.14, 0.14),
y = c(0.01, 0.01, -0.2, 0.07, 0.07, -0.2, 0.17, 0.17, -0.2),
Effect.size = factor(rep(c(
"small", "medium", "large"), each = 3
))
)
t.lab = c("0.01", "0.06", "0.14", "0.01", "0.07", "0.17")
x.lab = c(0.03, 0.08, 0.16, 0, 0, 0)
y.lab = c(0, 0, 0, 0.03, 0.08, 0.18)
g<- ggplot(dat, aes(
Eta.squared, Partial.eta.squared)
) +
geom_point() + theme_classic() +
theme(text = element_text(size = 14)) +
coord_cartesian(xlim = c(0, 0.3), ylim = c(0, 0.3))
g + geom_line(dat = df.1,
aes(x = x, y = y, color = Effect.size), size = 1.2) +
theme(legend.position=c(0.8, 0.5),
legend.justification=c(1,1)) +
annotate(
"text",label = t.lab,
x = x.lab, y = y.lab, size = 5)
########################
結果は,以下の図 1 のようになった。
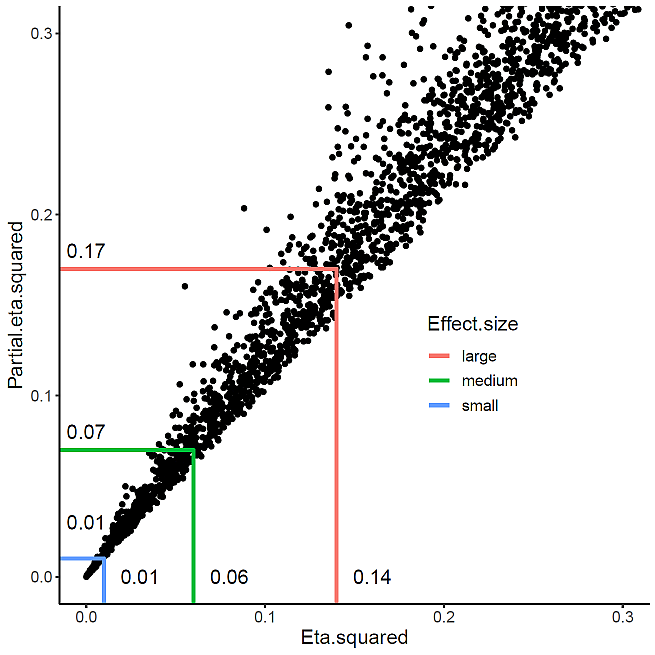
図 1. イータ二乗と偏イータ二乗の関係
理想的とも言える条件下だが,効果量が大きくなるほど,両者の数値が乖離することが分かる。しかし,大中小の基準を論じる範囲では,両者にそれほど差が無い。