ノンパラメトリック分散分析: Brunner-Munzel ANOVA
井口豊(生物科学研究所,長野県岡谷市)
最終更新: 2025 年 2 月 24 日
PDF version
DOI: 10.5281/zenodo.14916476
1. はじめに
非正規分布,不等分散のデータに適用されるノンパラメトリック検定として,よく知られたものが Brunner-Munzel 検定である。近年では, Mann-Whitney の U 検定よりも Brunner-Munzel 検定を優先的に使うべきだ,という意見も出ている。
Karch, J. D. (2021) Psychologists should use Brunner-Munzel’s instead of Mann-Whitney’s U test as the default nonparametric procedure. Advances in Methods and Practices in Psychological Science 4: 1–14.
日本の大学でも, U 検定に代わり Brunner-Munzel 検定の利用をもっと積極的に教えるべきだ。現状,国内でU 検定の脆弱性, Brunner-Munzel 検定の頑強性を明確に指摘しているのは, X (旧 Twitter)における黒木玄さんのコメントくらいかもしれない(X ポスト 2024-02-07 03:39)。この Brunner-Munzel 検定を複数要因の分散分析に適用したものが,統計ソフト R の rankFD パッケージにある Rank FD 分析である。このページのタイトルに Brunner-Munzel ANOVA と書いたが,正確には Brunner-Munzel タイプの ANOVA と言うべきかもしれない。パッケージのマニュアル Rank-Based Tests for General Factorial Designs の冒頭 Description に以下のように書かれている。
The rankFD () function calculates the Wald-type statistic (WTS) and the ANOVA-type statistic (ATS) for nonparametric factorial designs
文字通り,複数要因のノンパラメトリック分散分析である。非正規分布,不等分散のデータに対して,この関数によるノンパラメトリック分散分析は,私の共著,倉持・井口 (2020) の p.177 表 3 にも紹介されている。
まず単純な計算例として,次のような密度関数で表される母数 λ の指数分布を考える。
ここで λ = 2 として,それぞれ大きさ n = 30 の 2 標本(2 群)の相対効果(relative effect)の検定を, いわゆる Brunner-Munzel 検定と Rank FD 分析で比較してみる。
Brunner-Munzel 検定は,同じパッケージにある関数 rank.two.samples を使うと計算できる。相対効果の検定とは聞きなれないかもしれないが,最近の各種 R パッケージでは時々使われてる。このパッケージでも,今述べた rank.two.samples 関数の説明に以下のように書かれている。
testing whether the relative effect \( p = P (X < Y) + 1/2 * P(X = Y) \) of the two independent samples X and Y is equal to 1/2.
実行した Brunner-Munzel 検定と Rank FD 分析の R スクリプトは以下のとおり。
##########################################
library(rankFD)
set.seed(123)
y<- rpois(60, lambda = 2)
g<- factor(rep(1:2, each = 30))
dat<- data.frame(y, g)
# Brunner-Munzel 検定
rank.two.samples(y ~ g, data = dat)
# Rank FD 分析
rankFD(y ~ g, data = dat, hypothesis = "H0p")
########################################
結果を抜粋すると,以下のとおりで,どちらの計算でも, p 値は同じである。
################################################# # Brunner-Munzel 検定 Test Results: Effect Estimator Std.Error T Lower Upper p.Value p(1,2) 0.3844 0.0719 -1.6061 0.2404 0.5285 0.1137 # Rank FD 分析 ANOVA.Type.Statistic: Statistic df1 df2 p-Value g 2.5794 1 57.9169 0.1137 ###############################
2. 残差の正規性と等分散性のチェック
別ページにも書いたが,分散分析の正規性のチェックは,要因ごとに行うのではなく,分散分析モデル(一般線形モデル)の残差の正規性を調べるほうが良い。
さらに,等分散性にも注意する。以下の例では,一様連続分布のデータを利用した R による 分散分析(2 要因,各 2水準)の正規性と等分散性チェックである。検定するよりも,視覚的なチェックで十分である。例えば,以下の論文参照。
#############
# 分散分析残差の正規性と等分散性
set.seed(123)
dat <- data.frame(
A = factor(rep(1:2, c(15, 30))),
B = factor(rep(c(1:2, 1:2), c(5, 10, 10, 20))),
y = c(runif(15, 5, 15), runif(30, 0, 20))
)
AB.int<- interaction(dat$A, dat$B)
# 分散分析の線形モデル
mod <- aov(y ~ A*B, data = dat)
# 残差の正規 Q-Q プロットと等分散の確認
res <- mod$residuals
par(mfrow = c(1, 2))
qqnorm(res)
qqline(res, col="red")
plot(
res ~ AB.int,
xlab = "Level combinations",
ylab = "Residuals",
main="Residual plot"
)
################
結果は,次の図 1 のとおりである。
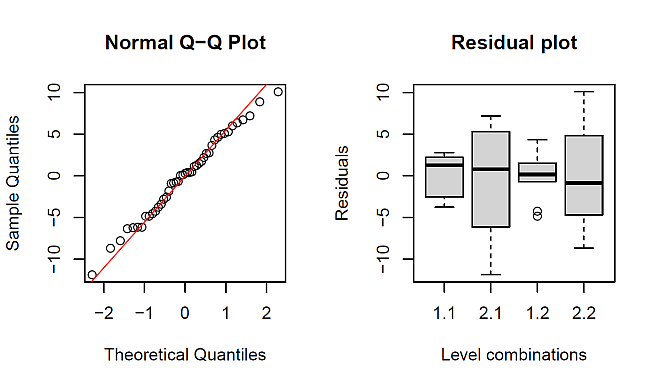
視覚的に,正規性または等分散性が満たされない可能性がある,と判断されれば, Rank FD 分析を実行する。
3. 二要因分散分析: 通常の ANOVA と Rank FD 分析
ここでは,以下の表 1 のように,母平均 10 で母分散が異なる一様連続分布を考えて,標本サイズが異なる 2 要因, 2 水準の対応のないデータによる分散分析(タイプ 3 平方和に設定)と Rank FD 分析を行い, p 値の出現状況を調べるシミュレーションをしてみる。
| 要因 | 母平均 | 母分散 | 標本サイズ |
|---|---|---|---|
| A1 B1 | 10 | 102/12 ≈ 8.3 | 5 |
| A1 B2 | 10 | 102/12 ≈ 8.3 | 10 |
| A2 B1 | 10 | 202/12 ≈ 33.3 | 10 |
| A2 B2 | 10 | 202/12 ≈ 33.3 | 20 |
以下が, R スクリプトである。ここでは要因 A の p の出現状況を例として計算してあるが,要因 B や A と B の交互作用の p 値も同様に計算できる。
#############
library(rankFD)
library(car)
library(Hmisc)
k<- 1e+4
set.seed(123)
g<- replicate(k, {
dat <- data.frame(
A = factor(rep(1:2, c(15, 30))),
B = factor(rep(c(1:2, 1:2), c(5, 10, 10, 20))),
y = c(runif(15, 5, 15), runif(30, 0, 20))
)
mod <- aov(
y ~ A*B,
data = dat,
contrasts = list(
A = contr.sum, B =contr.sum)
)
p.anova<- Anova(mod, type = 3)$Pr[2]
p.rankFD<- rankFD(
y ~ A*B, data = dat,
hypothesis = "H0p"
)$ANOVA.Type.Statistic[1, 4]
c(p.anova, p.rankFD)
})
#### グラフ化
pa<- g[1, ]
pr<- g[2, ]
par(mfrow = c(2, 2))
# 分散分析 p 値出現頻度ヒストグラム
hist(
pa, freq = FALSE,
xlab = "p value",
main = "ANOVA",
ylim = c(0, 1.5)
)
# Rank FD p 値出現頻度ヒストグラム
hist(
pr, freq = FALSE,
xlab = "p value",
main = "Rank FD",
ylim = c(0, 1.5)
)
# 経験累積分布関数(ECDF)
ck<- 1:k/k
d.1<- c(ck, pa)
d.2<- c(ck, pr)
test.1<- relevel(
factor(
rep(c("Theoretical", "ANOVA"),
each = k)
),
ref = "Theoretical")
test.2<- relevel(
factor(
rep(c("Theoretical", "Rank FD"),
each = k)
),
ref = "Theoretical")
# ANOVA
Ecdf(
d.1,
xlab="p value",
label.curves=list(keys= 1:2),
lty = 1:2,
col = c("black", "red"),
group = test.1,
main = "ECDF",
subtitles = FALSE
)
# Rank FD
Ecdf(
d.2,
xlab="p value",
label.curves=list(keys= 1:2),
lty = 1:2,
col = c("black", "red"),
group = test.2,
main = "ECDF",
subtitles = FALSE
)
################
結果は,次の図 2 のとおりである。
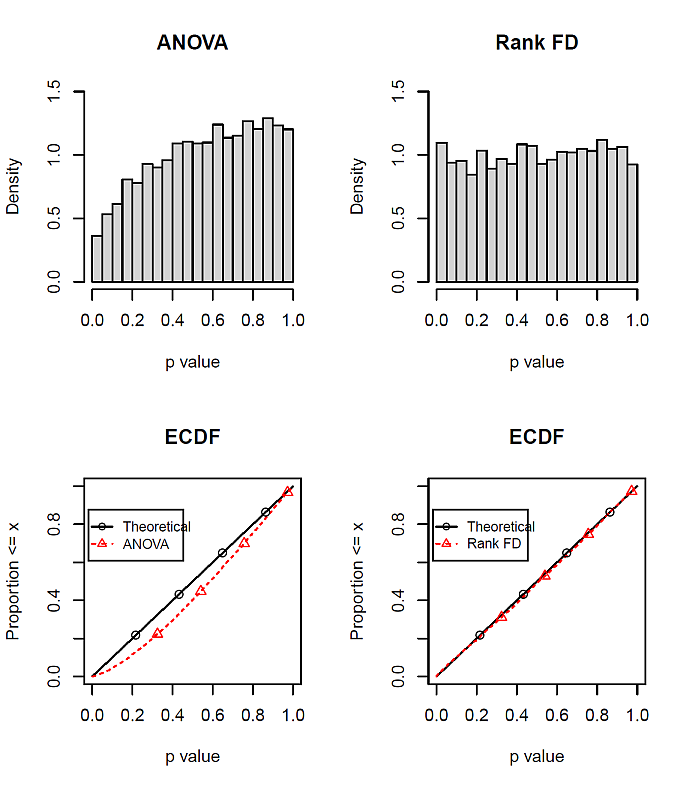
今回設定した条件の場合,通常のパラメトリック分散分析では, p 値が大きくなりがちだが,ノンパラメトリック ANOVA である Rank FD 分析は,ほぼ一様な p 値が出現する。非正規,不等分散のデータに対する Rank FD 分析が有用となる例である。