logo
生物科学研究所 井口研究室
Laboratory of Biology, Okaya, Nagano, Japan
Home

Friedman 検定の多重比較 Nemenyi 検定: 順位化対応あり t 検定

井口豊（生物科学研究所，長野県岡谷市）
最終更新： 2024 年 4 月 27 日

1. はじめに

Friedman 検定のあとの多重比較検定，いわゆる， post-hoc test として，しばしば使われる検定に，ネメニー検定（Nemenyi test）がある。 Wilcoxon-Nemenyi-McDonald-Thompson 検定とも呼ばれるものである。これは対応あるデータの多重比較検定である。

ただし，紛らわしいことに，対応のないデータの多重検定として使われるネメニー検定もあるので，注意が必要である。こちらは， Kruskal-Wallis 検定後の多重比較として，しばしば使われる。

例えば，統計ソフト R のパッケージ PMCMRplus の中では，上記の検定は，それぞれ frdAllPairsNemenyiTest と kwAllPairsNemenyiTest という関数で区別されているが，そうでなく，単に，ネメニー検定（Nemenyi test）と記されている場合は，注意が必要である。

なお， Friedman 検定や Kruskal-Wallis 検定で有意差が認められた後に多重検する，という手順自体も，検定の多重性という点で問題があり，不適切である。これらの検定結果とは別に多重検定するべきであり，分散分析の場合を例にして，別ページで既に述べた。

多重検定の基本的特徴あるいは適用条件を知るためには， 2 群（2 標本，サンプル数 2）の場合で計算してみると良い。多重検定は 3 群以上の検定であるかのように解説している教科書やサイトもあるが，本来は 2 群の検定がベースにある。そのことは，以下のページの Steel-Dwass 検定の例で触れた。

Friedman 検定に伴って使われるような，対応ある多重検定としての Nemenyi 検定は， 順位化された対応ある t 検定とほぼ同様な意味を持っている。ここでの順位化は，対応あるデータでの順位化であり，通常の対応ある t 検定と同じく，対応する順位データの差を取って検定する 1 標本（サンプル数 1）検定である。

ここでは，前述の Steel-Dwass 検定の場合と同様に，対応ある 2 群データを使って， Nemenyi 検定と順位化された対応ある t 検定の p 値の関係を統計ソフト R によるシミュレーションで確認してみよう。

2. 対応ある Nemenyi 検定と 順位化対応 t 検定の p 値の比較

対応する 2 群の 5 件法（5 段階）データを想定して，サンプルサイズ を 50 として，両検定の p 値を比較した。

以下が， R スクリプトである。 


#############

library(PMCMRplus)

n<- 50
k<- 1e+3 # 標本取り出し反復回数

p<- replicate(k, {

   # 対応ある（ペアとなる） 2 標本（5 段階データ）
   x<- sample(1:5, size = n, replace = TRUE)
   y<- sample(1:5, size = n, replace = TRUE)

   dat<- matrix(c(
   x, y
   ), nrow = n, ncol = 2, 
   dimnames = list(1:n, c("x", "y"))
   )

   rk<- apply(dat, 1, rank) # 対応あるデータ間の順位

   c(
   # 対応データ間で順位化された対応ある t 検定
    t.test(
      rk[1, ], rk[2, ], paired = TRUE
      )$p.value,

   # 対応ある Nemenyi 検定
   frdAllPairsNemenyiTest(dat)$p.value
   )
})

# 順位化された対応ある t 検定と
# 対応ある Nemenyi 検定の p 値

par(oma = c(3, 3, 2, 2))

plot(
  p[1, ], p[2, ],
  xlab = "Ranked paired t-test",
  ylab = "Nemenyi test",
  main = "P-value comparison",
  cex.lab  = 1.2,
  cex.axis = 1.0
)

abline(0, 1, col = "red")

################

結果は，次の図 1 のとおりである。

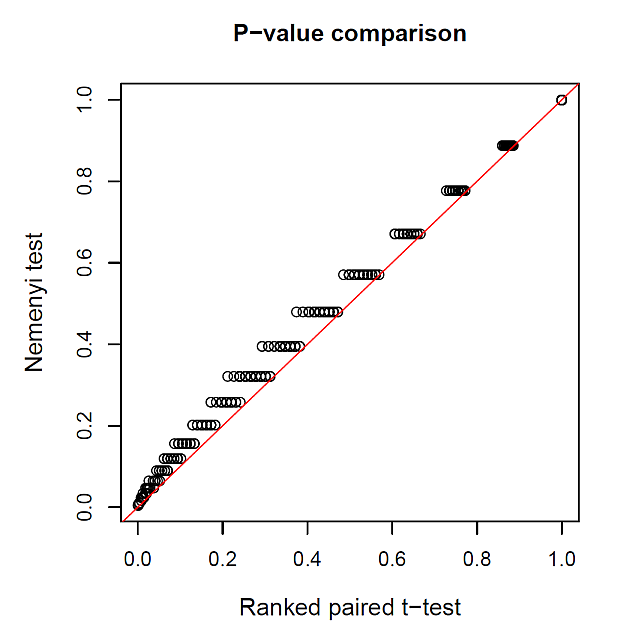
順位化された対応ある t 検定と対応ある Nemenyi 検定 p 値

図 1. p 値の比較: 順位化された対応ある t 検定と対応ある Nemenyi 検定

対応ある Nemenyi 検定の p 値が，順位化された対応ある t 検定の p 値より，やや大きくなるが，全体として，似たような p 値となることがわかる。これは， Friedman 検定が，対応ある分散分析（反復測定分散分析，あるいは，参加者内分散分析とも言う）のノンパラメトリック版であることを考えれば，当然とも言える。

Home