logo
生物科学研究所 井口研究室
Laboratory of Biology, Okaya, Nagano, Japan
Home

サーストンの一対比較法データを R で GLM 分析

井口豊（生物科学研究所，長野県岡谷市）
最終更新： 2022 年 10 月 19 日

1. はじめに

感性評価の一つの方法として，サーストンの一対比較法（Thurstone's paired comparison）がある。二つの評価対象から一つを選ぶ二者択一の回答方法である。論文でその結果を示すときは，一般的には，項目を直線上に並べて，どの項目が近いとか，遠いとか，そのような考察になる。その結果に統計学的な検定が伴うことは，あまりない。

このサーストン尺度（Thurstone scale）は，いわゆる二値データなので，誤差構造を二項分布とした一般化線形モデル（Generalized Linear Model, GLM）で分析できる。ここでは，統計ソフト R を用いたサーストン尺度の計算例を示す。正確に言えば，ケース Ⅴ を仮定した計算である。ケースについては，例えば，印東（1962）などを参照する。文献は最後に一括して挙げてある。

2. R によるサーストン尺度データの分析

データには，ちょっと古いが，それゆえ改めて計算してみる価値がある田畑ほか（1995） の p.447, Table 1 の 20 人の評価データを利用した。

R では，パッケージ eba の中の thurstone 関数が利用され，以下がその計算スクリプトである。なお，パッケージ psych の中に同名の関数があるので，関数同士が衝突しないように注意する。 


#############
# 項目間の選択比率データ
Input<- ("
A  B  C  D  E  F
0  0.2  0.3  0.5  0.2  0.1
0.8  0  0.2  0.8  0.3  0.3
0.7  0.8  0  0.7  0.5  0.3
0.5  0.2  0.3  0  0.3  0.1
0.8  0.7  0.5  0.7  0  0.3
0.9  0.7  0.7  0.9  0.7  0
")

dat<- read.table(
  textConnection(Input), header = TRUE
)*20 # 20 人の評価データ

library(eba)

mod<- eba::thurstone(dat)
mod # サーストン尺度と尤度比適合度検定

library("ggplot2")
library(ggrepel)

df.1<- data.frame(
 Estimate = mod$estimate,
 Item = rep(0, length(mod$estimate)),
 Name = names(mod$estimate)
)

g1<- ggplot(
    df.1,
     aes(x = Estimate, y = Item)) +
  geom_point(
  shape = 17,
  fill = "red", color = "red",
  size = 3
  ) +
  
  geom_text_repel(aes(label = Name)) +
  xlab("Thurstone Scale") +
  theme_classic() +
  coord_cartesian(ylim = c(0, 1), xlim = c(0, 1.5)) +
  theme(
    axis.line.y = element_blank(),
    axis.title.y = element_blank(),
    axis.text.y = element_blank(),
    axis.ticks.y = element_blank(),
)

plot(g1) # サーストン尺度値プロット

################

まず，統計モデルの適合度検定（尤度比検定）の出力結果を見て，適合していることを確認する。

G2(10) = 9.211, p = 0.5122

thurstone 関数のソースコードを見ると， glm の出力結果から，残差（逸脱度）を取り出して，カイ二乗検定していることが分かる。近似検定なので標本サイズが小さいと，あまり信頼できないとも言える。

各項目のサーストン尺度値は，次の図 1 のようになった。

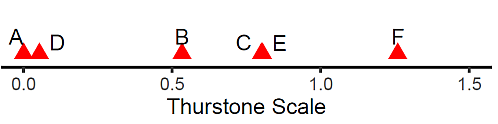
サーストン尺度値プロット

図 1. サーストン尺度値プロット

田畑ほか（1995） の p.447, Table 1b の図と比べると，項目の並び順は逆になっているが，それぞれの相対的な間隔距離は，同じ結果となっていることが分かる。

次に， GLM の結果を示す。 


#############
mod<- eba::thurstone(dat)
summary(mod$tm.glm) # A 項目を参照とするGLM の結果

# 95% 信頼区間
est<- mod$estimate[2:6]
ci<- confint.default(mod$tm.glm)

low<- ci[, 1]
up<- ci[, 2]

comp<- c(
  "A-B", "A-C", "A-D", "A-E", "A-F"
)

df<-data.frame(
  est, up, low, comp
)

library("ggplot2")

# 項目間の差と信頼区間グラフ
g2<- ggplot(df, aes(comp, est)) + 
    geom_point() +
    geom_errorbar(aes(ymin = low, ymax = up)) +
    ggtitle("Cmparison of Thurstone scale values") +
    xlab("Comparison") +
    ylab("Mean difference (95% CI)") +
    geom_hline(
       yintercept = 0, linetype = "dashed", 
       color = "red"
    ) +
    theme_classic()

plot(g2)

################

まず GLM の計算結果は，次の図 2 のとおりである。

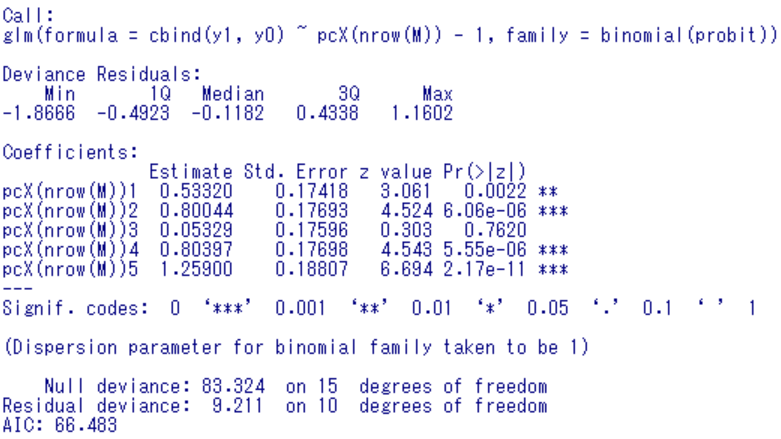
GLM結果

図 2. GLM 結果

出力の右上を見ると，
family = binomial(probit)
となっていて， probit 関数，つまり，標準正規分布の累積分布関数の逆関数が使われていることが分かる。これが，サーストン尺度値の計算の特徴である。

さらに， GLM の係数が， A を参照項目としたときの，各項目とのサーストン尺度値の差，つまり，前述のサーストン尺度値（図 1）そのものであることが分かる。

3 番目の係数，つまり， A と D の差だけが有意でないことも分かる。

次に，この尺度値の差に信頼区間を付けて表したのが，次の図 3 である。

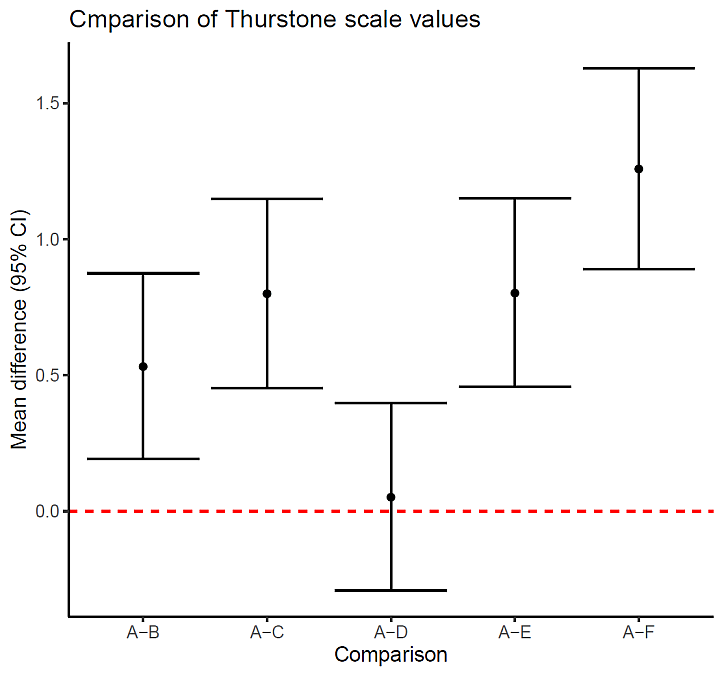
サーストン尺度値の比較

図 3. サーストン尺度値の項目間比較比較

A と D の差の信頼区間だけ，ゼロをまたいでいて，ここからも有意差が無いことが分かる。

関連サイト

参考文献

Home