Scilab と R による 3D 散布図と回帰平面

井口豊（生物科学研究所，長野県岡谷市）
最終更新：2024 年 5 月 8 日

1. はじめに

久しぶりに Scilab を使ってみた。 R を使うことが多いため，うっかりすると，スクリプトを混同してしまうので，基本的な使い方を再確認する意味でも，たまには， Scilab を使うべきだと実感した。ここに書いた 3 次元グラフでは，私は gnuplot を使い発表することが多いし，最近もそうだった（井口，2019）。 Scilab の難点として， gnuplot に比べて，作図の時間も長めとなるからだ。

ここでは，3 次元データの散布図と，それに対する重回帰平面の適合について紹介する。このような作図は，よくありそうで，意外と無かった。ここで言う，重回帰平面とは，二変数 x, y を説明変数， z を目的変数とする回帰式が表す 3 次元平面である。

これを回帰直線と呼ぶ人がいるが，文字通り，回帰平面と呼ぶべきであり，それを Scilab で作図した例を示す。

2. Scilab による重回帰式フィット

Scilab による重回帰式のフィットには， reglin 関数を使う。 R で一般的に見られるように，各変数を明示的に入れるなら， Scilab でも以下のようなスクリプトになる。

reglin(x, y, z)

これでも計算されるのだが， Scilab の場合，回帰式を適切にフィットさせるためには， x, y は，ひとまとめにして行列データ X として扱われる。実際， reglin のオンラインマニュアルにも，そう書かれている。

reglin(X, z)

この点をまずチェックして見よう。大きさ 100 の標本で， x, y を正規乱数として， z を以下の式から算出する。

この x, y, z データを使って，逆に，回帰式を推定し，元の係数が復元されるかどうか調べるのである。

// スクリプト開始
n = 100;
rand("seed", 10)

x = rand(1, n, "normal");
y = rand(1, n, "normal");
z = 2*x - y + 3;

// 最小2乗フィット
// 明示的に x, y を与えた場合
[p, q, r] = reglin(x, y, z)

// x, y を行列データとした場合

X = [x; y];

[A, c] = reglin(X, z)
// スクリプト終了

結果は，以下のようになった。

明示的に x, y を与えた場合
p = - 0.0227378
q = - 0.1204544
r = 0.9328821

x, y を行列データとした場合
A = 2, - 1
c = 3

これで， Scilab による重回帰では x, y を行列データにするべきだと確認できた。その上で，改めて，この結果を 3 次元グラフとして描画して見る。

// スクリプト開始
n = 100;
rand("seed", 10)

x = rand(1, n, "normal");
y = rand(1, n, "normal");
z = 2*x - y + 3;

// 最小2乗フィット
X = [x; y];

[A, c] = reglin(X, z)

// データ最大・最小確認
max(X, 'c')
min(X, 'c')

// 空間メッシュ
[xx, yy] = meshgrid(-3:0.4:3, -3:0.4:3);

// 重回帰式
zz = A(1)*xx + A(2)*yy + c;

// 既存グラフのクリア
clf()

// 3次元散布図
scatter3d(x, y, z, "fill");

// 軸ラベル
sz = 5
xlabel("X", "fontsize", sz);
ylabel("Y", "fontsize", sz);
zlabel("Z", "fontsize", sz);

// 回帰平面
surf(xx, yy, zz, 'facecol','yellow','edgecol','red')
// スクリプト終了

その結果，出力されたグラフが初期状態で，次の図 1 である。

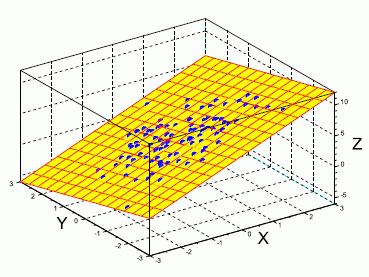
グラフは，マウスの右クリックで，グルグルと自由に回転できる。例えば，回帰平面の垂直断面図は，次の図 2 のようになる。

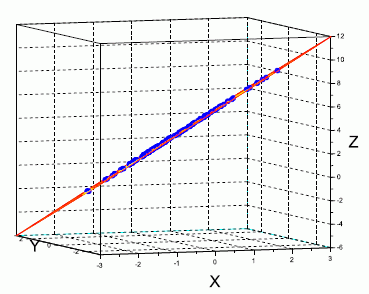
データ点が，回帰平面上に分布していることが，一目瞭然である。

3. R による重回帰式フィット

R で似たような機能を持つ関数として， car パッケージの scatter3d 関数がある。それと rgl パッケージを使うと，以下のようなスクリプトになる。

## スクリプト開始
library(car)
library(rgl)

x<- rnorm(100)
y<- rnorm(100)
z<- 2*x - y + 3

par3d(cex=1.2)

scatter3d(
 axis.col=c("black", "black", "black"),
 axis.scales=T,
 x=x, y=z, z=y, residuals=F,
 xlab="X", ylab="Y", zlab="Z"
)

rgl.snapshot("r-scatter3d-regression.png", fmt="png")
## スクリプト終了

その結果，出力されたグラフが次の図 3 である。

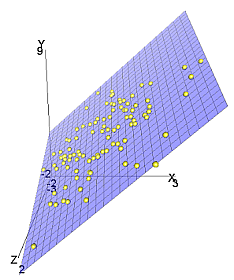
3 次元回帰平面に関する限り， R のほうがオプションの指定が面倒だ。

参考文献

井口豊 (2019)
諏訪盆地西部における御岳第一テフラの高度分布
日本地理学会発表要旨集 96: 124（2019 年度日本地理学会秋季学術大会）.