生物科学研究所 井口研究室
Laboratory of Biology, Okaya, Nagano, Japan
ログランク検定の統計量の計算
井口豊(生物科学研究所,長野県岡谷市)
最終更新: 2024 年 7 月 7 日
1. ログランク検定の統計量
生存解析でよく知られたログランク検定の検定統計量は,カイ二乗値である。ここでは,最も簡単な二群のログランク検定の計算を解説する。
2. データ
以下の表 1 に示した仮想データを考える。
3. R によるログランク検定
まず,統計ソフト R で上記データをログランク検定してみる。イベントが発生した度数(人数)が超幾何分布に従うことを利用して,その分散が計算に使われる。これは, R のパッケージ safestats で容易に算出できるので,それを利用する。スクリプトは以下のとおり。
##############################################
Input<- ("
time event group
4 1 A
6 1 B
19 1 A
23 1 A
36 1 A
36 1 B
40 0 A
40 0 A
40 0 B
40 0 B
")
dat<- read.table(
textConnection(Input), header = TRUE
)
library(survival)
# ログランク検定
Lr<- survdiff(Surv(dat$time, dat$event) ~ dat$group)
Lr
# カイ二乗検定統計量
Lr$chisq
# 超幾何分布分散
library(safestats)
res<- computeLogrankZ(
Surv(dat$time, dat$event), dat$group)
res$varVector
##############################################
結果は,以下のとおりである。
#####################################################
N Observed Expected (O-E)^2/E (O-E)^2/V
dat$group=A 6 4 3.35 0.125 0.307
dat$group=B 4 2 2.65 0.159 0.307
Chisq= 0.3 on 1 degrees of freedom, p= 0.6
# カイ二乗検定統計量
Lr$chisq
0.3073699
# 超幾何分布分散
result$varVector
0.2400000 0.2469136 0.2343750 0.2448980 0.4000000
###################################################
4. ログランク検定の統計量の計算
ログランク検定の検定統計量を計算する手順を具体的に考えてみる。まず,表 1 のデータを並び替えて,計算を加えたのが,次の表 2 である。ここで, nA, nB は 2 群 A, B それぞれの時点の人数であり, OA, OB,は実際にイベントが認められた人数, EA, EB は,予期された人数(期待値)である。期待値は,以下のように求められた。
\begin{align}
E_A = (O_A + O_B)\frac{n_A}{n_A + n_B} \\
E_B = (O_A + O_B)\frac{n_B}{n_A + n_B}
\end{align}
さらに,表下部の ΣOA, ΣOB, ΣEA, ΣEB, ΣV は,それぞれ OA, OB, EA, EB, V の期間内の(表の縦方向の)数値の総和を表す。 V は,さきほど R で計算された超幾何分布の分散である。
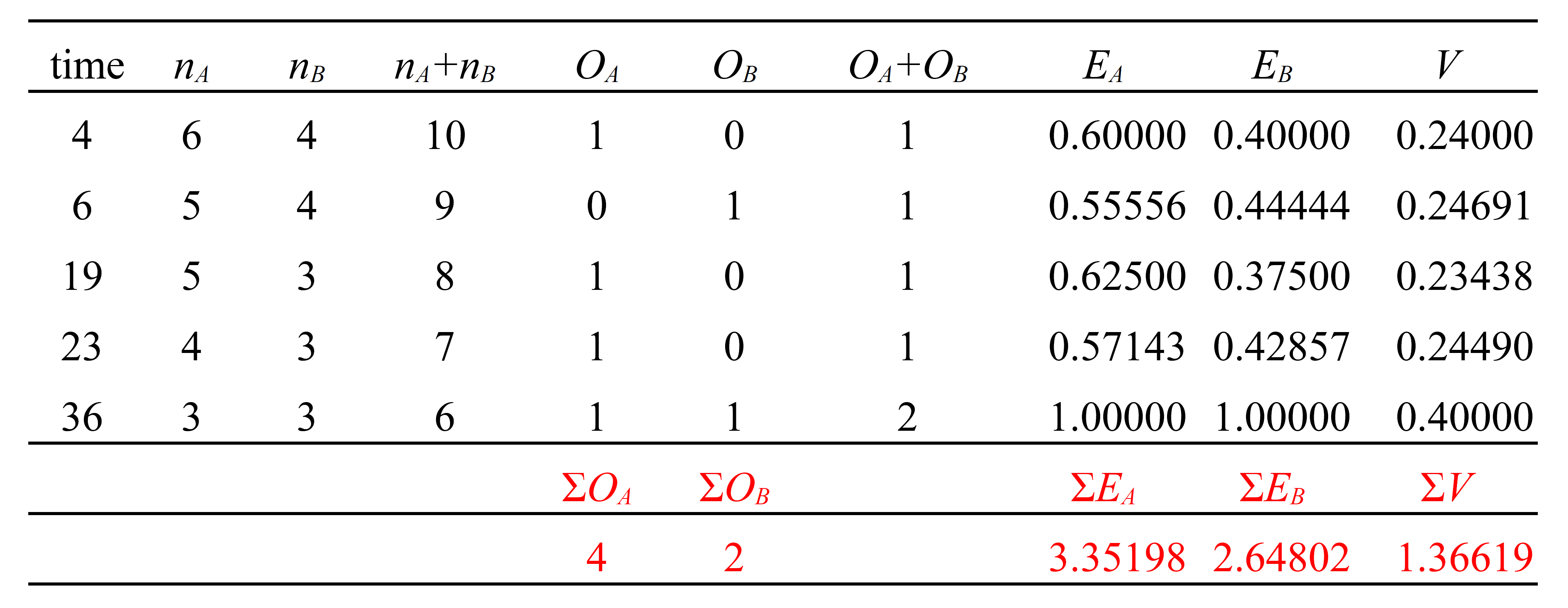
ログランク検定の検定統計量であるカイ二乗値は,表の下部に算出された観察値,期待値,分散のそれぞれの総和を使って,以下のようにして計算される。
A 群の総和から,
\begin{align}
\chi^2 &= \frac{(\sum O_A - \sum E_A)^2}{\sum V} \\
&= \frac{(4 - 3.35198)^2}{1.36619} \\
& = 0.30737
\end{align}
または B 群の総和から,
\begin{align}
\chi^2 &= \frac{(\sum O_B - \sum E_B)^2}{\sum V} \\
&= \frac{(2 - 2.64802)^2}{1.36619} \\
& = 0.30737
\end{align}
どちらでも同じ結果であり,前述の R の算出結果とも同じである。