Kruskal-Wallis は平均順位検定であり，中央値検定ではない
井口豊（生物科学研究所，長野県岡谷市）
最終更新： 2022 年 10 月 29 日
1. はじめに
データ分布の位置（location）に関するノンパラメトリック検定となると，すぐに中央値の検定と思われるようで， Kruskal-Wallis （クラスカル・ウォリス）検定もその一つである。しかし実際には，この検定は平均順位（mean rank, 順位平均とも言う）の検定と言うべきであり，特に，標本サイズが大きい場合の近似計算では，平均順位を比較する分散分析（Rank ANOVA）そのものとも言える。
ここでは， R を使い，シミュレーションで Kruskal-Wallis 検定，中央値検定，順位データの分散分析の p 値を比較してみた。
なお，Kruskal-Wallis 検定を 2 群で計算すると， Mann-Whitney U 検定の結果となる（Kruskal-Wallis 検定を使えば U 検定は不要：漸近と正確検定）。したがって， U 検定もまた平均順位検定である。
パラメトリック検定である分散分析を 2 群で計算すると， t 検定の結果となる（対応ある t 検定は 1 群検定，分散分析は 2 群以上の検定）。この両者が母平均の検定であることと， Kruskal-Wallis 検定と Mann-Whitney U 検定が平均順位検定であることは，同様な関係にある。
2. Kruskal-Wallis 検定，中央値検定，順位分散分析
便宜上，同点（タイ）を避けるために，連続一様乱数を使い， 3 群（サンプル数 3），それぞれ大きさ 50 （サンプルサイズ 50）とした。
中央値検定には，パッケージ coin の median_test 関数（Brown-Mood median test）を使った。
以下が， R スクリプトである。
#############
library(coin)
k<- 1e+2 # 標本取り出し反復回数
n<- 50
grp<- factor(rep(1:3, each = n))
p<- replicate(k, {
dat<- runif(3*n, 1, 5)
c(
kruskal.test(dat ~ grp)$p.value,
pvalue(median_test(dat ~ grp)),
oneway.test(rank(dat) ~ grp, var.equal = TRUE)$p.value
)
})
par(oma = c(3, 3, 2, 2))
# Kruskal-Wallis 検定と中央値検定
plot(
p[1, ], p[2, ],
xlab = "Kruskal-Wallis test p-value",
ylab = "Mood's median test p-value",
cex.lab = 1.2,
cex.axis = 1.0
)
abline(0, 1, col = "red")
# Kruskal-Wallis 検定と順位分散分析
plot(
p[1, ], p[3, ],
xlab = "Kruskal-Wallis test p-value",
ylab = "Rank ANOVA p-value",
cex.lab = 1.2,
cex.axis = 1.0
)
abline(0, 1, col = "red")
################
結果は，次の図 1 のとおりである。
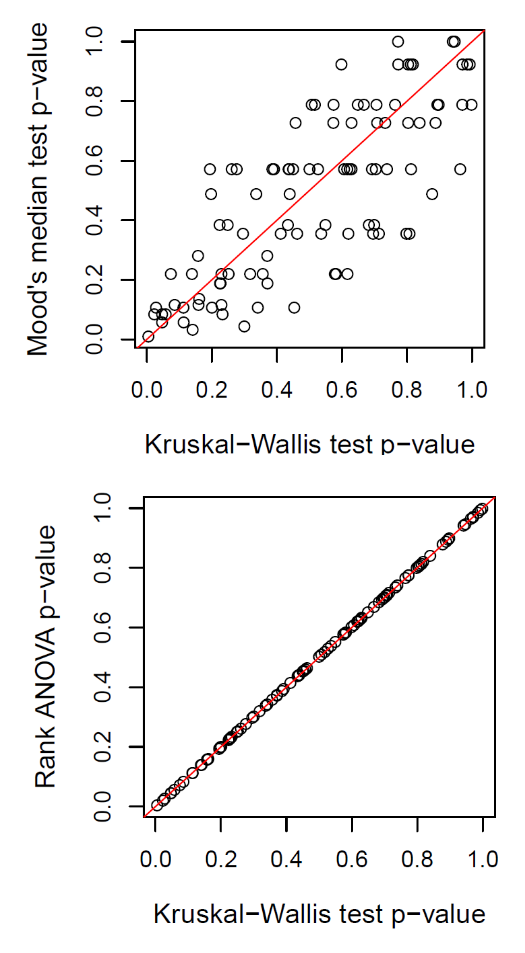
Kruskal-Wallis 検定の p 値が，中央値検よりも，順位分散分析のそれに近いことが分かる。
論文の記載例
鈴木ほか（2006）， p.182 表 2 には，中央値と四分位範囲が示されている。これ自体は，一般に見られることだが，これとは別に，次ページの表 3 には， Kruskal-wallis の検定結果とともに，各群の平均順位が示されている。本来，このように平均順位も記したほうが良いのである。
新型コロナ関連の研究で， Alhowaymel et al. (2022), p.6 Table 3 には， Mann-Whitney U 検定と Kruskal-Wallis 検定の結果とともに，平均，標準偏差，平均順位（Mean rank）が記されている。このように， U 検定も Kruskal-Wallis 検定も，平均順位を記したほうが良いのである。
関連サイト
参考文献
Alhowaymel, Abaoud, Alhuwaimel, Alenezi and Alsayed (2022) COVID-19 Patients'Satisfaction Levels with Nursing Care: A Cross-Sectional Study. SAGE Open Nursing 8.
印東太郎（1962）サーストンの心理尺度構成法. 日本音響学会誌 18(1): 16-22.
鈴木亨・園田茂・才藤栄一・村田元徳・清水康裕・三沢佳代（2006） 回復期リハビリテーション目的の入院脳卒中患者における転倒, 転落事故と ADL. リハビリテーション医学 43(3): 180-185.