Kruskal-Wallis 検定：近似検定の標本サイズ
井口豊（生物科学研究所，長野県岡谷市）
最終更新： 2022 年 10 月 23 日
1. はじめに
ノンパラメトリック検定の Kruskal-Wallis 検定で，しばしば近似計算が使われるが，それに気づかないで利用しているケースがあることは，既に別ページで指摘した。
例えば， 3 群の場合，まずデータ全体の順位を計算し，その中から，各群内の順位和 R1, R2, R3 を取り出し，以下の式に基づいて，検定統計量 H を求める。ここで N は全体の標本サイズ， n1, n2, n3 は各群の標本サイズである。
\[ H=\frac{12}{N(N+1)}\biggl(\frac{R_1^2}{n_1}+\frac{R_2^2}{n_2}+\frac{R_3^2}{n_3} \biggl)-3(N+1) \]この統計量 H が，標本サイズが大きくなるにつれて，群数 − 1 の自由度（ここでは， 3 − 1 = 2） のカイ二乗分布に近似的に従うことを利用して p 値が算出される。
当然ながら，小標本の場合は，この近似が適用できないので， Kruskal-Wallis 正確検定ということになる。しかし実際には，統計ソフト R の場合， coin パッケージ LocationTests 関数マニュアルに書かれたように， kruskal_test で， distribution に "approximate" を指定して，モンテカルロ法での計算になる。
実際に，前述のサイトで扱った医学論文の場合（学術論文で気になるケース）， 4 群 22 症例の Kruskal-Wallis 検定で有意差無し，となっていた項目を，掲載データを使って Kruskal-Wallis 正確検定で再計算したところ，有意差あり，となった。
では，近似計算を使う場合，どのくらいの標本サイズが必要だろうか？シミュレーションで調べてみた。
2. Kruskal-Wallis 検定統計量 H 近似と標本サイズ
ここでは，いわゆる 5 件法， 5 段階リッカート尺度（Likert scale）を想定してみた。 1 から 5 の整数値が，母比率 2:4:2:1:1 である集団を考え，大きさ 5, 10, 20, 30, 50, 100 の標本を 10 万回繰り返し取り出し， H を計算し，自由度 2 のカイ二乗分布との適合度を Q-Q plot で調べた。検定と並び替え検定を行い， p 値の出現状況を調べるシミュレーションをしてみる。
以下が， R スクリプトである。パッケージ EnvStats の qqPlot 関数が使われている。
#############
k<- 1e+5 # 標本取り出し反復回数
n<- c(5, 10, 20, 30, 50, 100)
h<- hn<- as.numeric(NULL)
for (i in 1: length(n)) {
h<- replicate(k, {
grp<- factor(rep(1:3, each = n[i]))
dat<- sample(
1:5, 3*n[i], prob = c(2, 4, 2, 1, 1),
replace = TRUE)
kruskal.test(dat ~ grp)$statistic
})
hn<- c(hn, h)
}
hmat<- matrix(hn, ncol = length(n))
head(hmat)
library(EnvStats)
qq<- function(x) {
qpt<- qqPlot(
x, dist = "chisq",
param.list=list(df = 2),
add.line = TRUE,
line.col = "red",
line.lwd = 2,
equal.axes = TRUE,
ylab ="Observed quantiles",
main = "Chi−square Q−Q Plot \n
for K-W test with 3 groups"
)
}
par(mfrow = c(3, 2))
qq(hmat[, 1])
text(10, 20, "Each group with n = 5")
qq(hmat[, 2])
text(10, 20, "Each group with n = 10")
qq(hmat[, 3])
text(10, 20, "Each group with n = 20")
qq(hmat[, 4])
text(10, 20, "Each group with n = 30")
qq(hmat[, 5])
text(10, 20, "Each group with n = 50")
qq(hmat[, 6])
text(10, 20, "Each group with n = 100")
################
結果は，次の図 1 のとおりである。
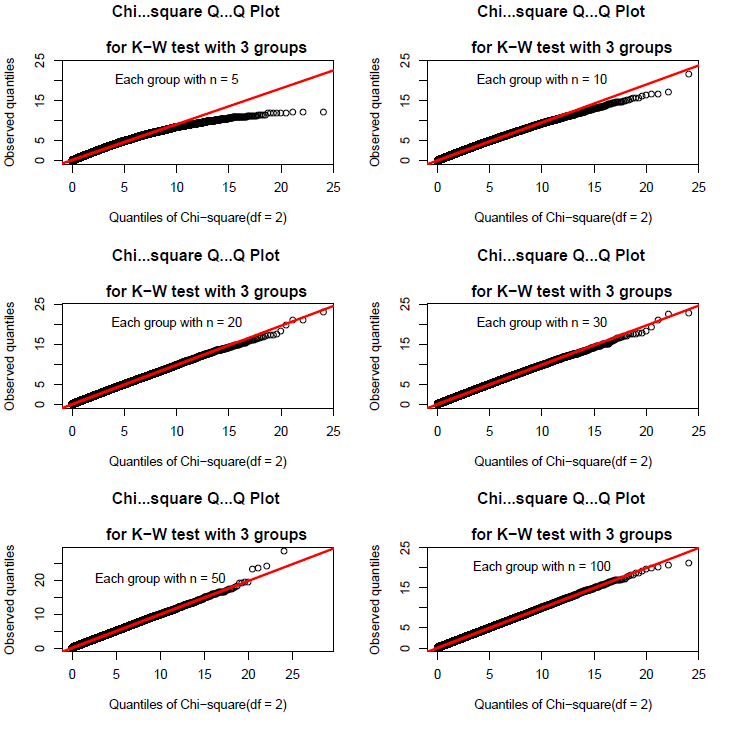
Kruskal-Wallis 検定統計量 H の近似計算を適用するためには， 1 群あたり標本サイズ n が，少なくとも 20 程度，出来れば 50 程度欲しいのである。もちろん，これ以外の条件になれば結果も変わってくる。
逆に言えば， 1 群あたり 10 個前後のデータで， Kruskal-Wallis 検定の近似計算に気づかないと問題になるかもしれない。
実際，冒頭で指摘した医学論文の場合（学術論文で気になるケース）， 4 群 22 症例の Kruskal-Wallis 検定で，おそらく近似検定だったために，正確検定で再計算した結果と異なった可能性がある。