円の最小2乗近似と描画にRのoptimxとdraw.circle関数

井口豊（生物科学研究所，長野県岡谷市）
最終更新：2023 年 12 月 29 日

ウェブ上を見ていて，意外に解説が少ないのが，円の最小2乗近似の方法であった。以下のページには， Excel を使った方法が述べられている。

• 一般式による最小二乗法（円の最小二乗法）
• 半径の２乗の差の総和をゼロとする方法（教えて!goo 最小二乗法公式のベストアンサー）

しかし，これらは，「中心から各点への距離の2乗」と「円の半径の2乗」の差を最小化しようとしているため，実態に合わない円の近似となってしまう。

ここでは，実際に 8 個の点
(3, 0), (5, 0), (0, 3), (0, 5), (-3, 0), (-5, 0), (0, -3), (0, -5)
に対する円の近似を統計解析ソフト R を使い，まず直感的に考えてみよう。

x<- c(3, 5, 0, 0, -3, -5, 0, 0)
y<- c(0, 0, 3, 5, 0, 0, -3, -5)
plot(x, y, asp=1, col="magenta")

あとで近似円を描きやすいように，アスペクト比（asp）を 1 にしてある。

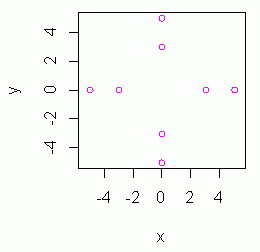
この散布図ならば，中心 (0, 0)，半径 4 の円が描けると推定される。

ここで重要なことは，通常最小二乗法（Ordinary Least Square: OLS）は，y方向の値しか最小化しないため，円の近似には妥当でない，ということである。この通常最小 2 乗法の計算については，実は，大学の研究者でも知らない人がいるので注意が必要である。この点に関しては，私のウェブ解説も参照: 回帰と相関，知っているようで知らない，その本質。

R を使って円を描く場合は，パッケージ plotrix の中の draw.circle 関数やパッケージ shape の中の plotcircle 関数を使えば，円が簡単に描画できる。

ここでは，draw.circle 関数を使う。 plot 関数から，再度書くと，以下のようになる。

plot(x, y, asp=1, col="magenta")
library(plotrix)
draw.circle(0, 0, 4) # 中心 (0, 0)，半径 4 の円

実に簡単，1行で円を描くスクリプトが書ける。

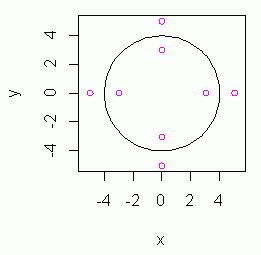
その上で，中心から各点までの距離と半径の差を最小 2 乗化するために，パッケージ optimx の中の optimx 関数を利用する。この関数の利点は，オプション all.methods=T を指定すると，多くの近似法の結果を返してくれる点である。それを適合度が高い（残差が小さい）順に並べれば良い。初期値として，中心 (1, 1)，半径 5 として計算したのが次のスクリプト。

f<- function(arg) {
  a<- arg[1]
  b<- arg[2]
  r<- arg[3]
  t<- (sqrt((x-a)^2 + (y-b)^2)-r)^2
  return(sum(t))
}

library(optimx)

res<- optimx(
  c(1, 1, 5), # 初期値，中心 (1, 1)，半径 5
  f, control=list(all.methods=T) # 全ての近似法
)

summary(res, order=value) # 残差が小さい順に示す

必要部分だけ，結果を示す。

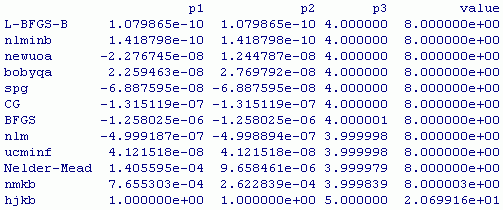
L-BFGS-B法がベストな方法で，中心 (0, 0)，半径 4 の円で近似されるだろうと推定される。 初期値，中心 (0, 0)，半径 4 として，再度計算させる。

f<- function(arg) {
  a<- arg[1]
  b<- arg[2]
  r<- arg[3]
  t<- (sqrt((x-a)^2 + (y-b)^2)-r)^2
  return(sum(t))
}

res<- optimx(
  c(0, 0, 4), # 初期値，中心 (0, 0)，半径 4
  f, control=list(all.methods=T) # 全ての近似法
)

summary(res, order=value) # 残差が小さい順に示す

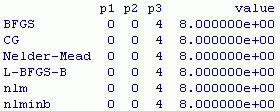
今度は，すっきりした結果が出た。