logo
生物科学研究所 井口研究室
Laboratory of Biology, Okaya, Nagano, Japan
Home

AIC と BIC，その特徴を比較

井口豊（生物科学研究所，長野県岡谷市）
最終更新：2019年11月14日

1. はじめに

多変量の回帰分析で，変数選択基準として用いられる代表的手法に AIC (Akaike information criterion, 赤池情報量規準) と BIC (Bayesian information criterion, ベイズ情報量規準) がある。

ところが，これら 2 種類の基準について，実際にどのような特徴があるのか説明した例は少ない。理論的な解説は，AIC を考案した赤池の以下の論文を読むと良い。

赤池弘次 (1996)
AIC と MDL と BIC
オペレーションズ・リサーチ 41(7): 375-378.

ここでは，実際に適用するときに，両者でどのような違いが出るのか，シミュレーションしてみる。

2. 統計ソフト R による変数選択シミュレーション

通常の重回帰分析を取り上げても良いが，ここでは敢えて，目的変数が二値であるロジスティック回帰分析の変数選択をシミュレーションしてみる。

説明変数を 5 個の正規乱数として，定数項を含め，計 6 個のパラメータをロジスティック回帰で推定する1000回の反復計算を行なった。パッケージ bestglm を用いて， AIC と BIC で変数選択をおこない，何個の説明変数が残るか計算した。

以下に，Rによるシミュレーションのスクリプトを書く。 

library(bestglm)
n<- 1000

np<- replicate(n, {

  y <- sample(0:1, 100, replace=T)
  x<- matrix(rnorm(500), ncol=5)

  Xy<- data.frame(x, y)

  suppressMessages(
   c(
    length(bestglm(Xy, family=binomial(link="logit"),
    IC="AIC")$BestModel$coefficients),

    length(bestglm(Xy, family=binomial(link="logit"),
    IC="BIC")$BestModel$coefficients)
    )
  )

})

AIC.npar<- hist(np[1, ], breaks=seq(0.5, 6.5, 1))$counts
BIC.npar<- hist(np[2, ], breaks=seq(0.5, 6.5, 1))$counts

dat<- rbind(AIC.npar, BIC.npar)
rownames(dat) <- c("AIC", "BIC")
colnames(dat) <- c("1", "2", "3", "4", "5", "6")
dat

barplot(
 dat, ylim=c(0, n),
 xlab="Number of variables including a constant term selected",
 beside=T, legend=T, col=c("#ff00ff", "#0080ff"),
 main="Variable selection in five-variable logistic regression"
)

結果として，選択された説明変数の個数分布（図 1）を見ると， AIC のほうが BIC よりも多くの説明変数が残る傾向があると分かる。ただし，乱数データなのだから，本来は，BIC の結果のように定数項 1 個だけが残るほうが正しい，という逆説的な見方も可能である（厳密に言えば，今回の結果で，その 1 個が定数項とは限定されないが）。

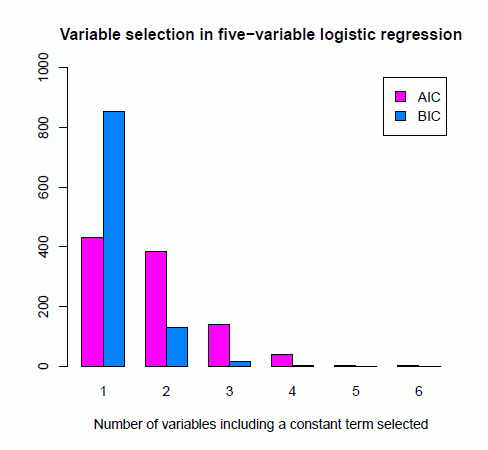
ロジスティック回帰変数選択をAICとBICで実行した結果

図 1. 5 変数ロジスティック回帰を AIC と BIC で変数選択し，残された説明変数個数

これについては，最初に挙げた赤池（1996）論文が，最後の部分で，以下のように結論していることとも符合する。

BIC は，有意なパラメータと，そうでないものとが，容易に識別できる状況に対応するモデルから得られ，これに対してAICは，有意性がようやく認められる程度のパラメータの取り扱いに注目し，誤差の影響に埋没しそうになるところまでモデル化の可能性を追及

参照：赤池弘次 (1996) AIC と MDL と BIC (p. 378)

得られたデータの統計解析の実践的な場面で， AIC と BIC のどちらを使うか迷うときの指針にもなりうる赤池の説明である。

3. 終わりに

AIC は，故・赤池弘次が残した情報理論に関する，日本が世界に誇る業績であり，それにより赤池は，2006 年に第 22 回京都賞を受賞している。私も AIC を利用した統計問題を解説したので，そちらも参照して欲しい。

決定係数 R2 の違い: Excel, OpenOffice, LibreOffice および統計解析ソフト R を用いて

さらに，コクワガタ雄の大顎の三型を統計解析したときも， AIC を使った。

Iguchi Y (2013)
Male mandible trimorphism in the stag beetle Dorcus rectus (Coleoptera: Lucanidae) European Journal of Entomology, 110: 159-163.

Home