Mann-Whitney U 検定と並べ替え検定：小標本の正確検定

井口豊（生物科学研究所，長野県岡谷市）
最終更新： 2022 年 9 月 22 日

1. はじめに

ノンパラメトリック検定の代表格とも言える Mann-Whitney U 検定（Wilcoxon 順位和検定）で，大標本の場合（標本サイズ n が大きい場合）は正規近似計算される。すなわち，二つの標本（2 群，サンプル数 2）の大きさをそれぞれ n₁, n₂ とすると，それらが大きくなるにつれ，検定統計量 U は，次のような平均 E，分散 V の正規分布に近づく。

\[ E=\frac{n_1n_2}{2} \] \[ V=\frac{n_1n_2(n_1+n_2+1)}{12} \]

当然ながら，小標本の場合は，この近似が適用できないので，正確 U 検定を使うというのが常套手段である。しかし，それで本当に良いのだろうか？ここでは，同じく小標本の検定に使われる並び替え検定（Permutation test）の計算結果と比較してみた。

2. 小標本の正確 U 検定と並び替え検定シミュレーション

ここでは，いずれも大きさ 10 の二標本を平均 50，分散 1 の正規母集団から 10 万回繰り返し取り出し，正確 U 検定と並び替え検定を行い， p 値の出現状況を調べるシミュレーションをしてみる。

以下が， R スクリプトである。

#############
library(exactRankTests)
library(perm)

n<- 5
k<- 1e+5

g<- replicate(k, {

 x<- rnorm(n, mean = 50, sd = 1)
 y<- rnorm(n, mean = 50, sd = 1)

 c(
 # 並び替え検定
 permTS(
   x, y, method = "exact.mc",
   control = permControl(setSEED = FALSE)
   )$p.value,

 # 正確 U 検定
 wilcox.exact(x, y, exact = TRUE)$p.value
)

})

pp<- g[1, ]
pw<- g[2, ]

par(mfrow = c(2, 1))

# 並べ替え検定 p 値出現頻度ヒストグラム
hist(
  pp, freq = FALSE,
  xlab = "p value",
  main = "Permutation test"
)

# 正確 U 検定 p 値出現頻度ヒストグラム
hist(
  pw, freq = FALSE,
  xlab = "p value",
  main = "Exact Mann-Whitney U test"
)

################

結果は，次の図 1 のとおりである。

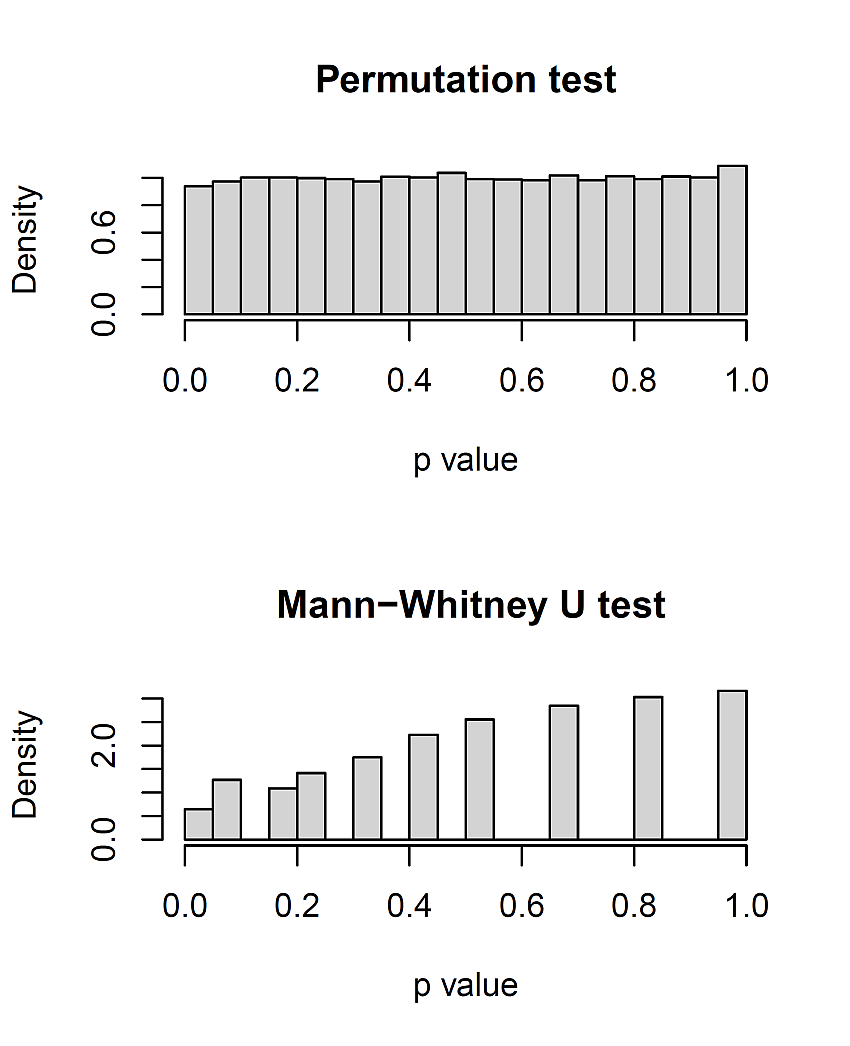
正確 U 検定では正しく棄却されず，より大きな p 値が出やすくなってしまうことが一目瞭然である，という思い込みは，非常に危ない！ という指摘が，黒木さんのツイート ヒストグラムはビンの取り方で印象が大幅に変わるので要注意 であった。

飛び飛びの値のヒストグラムを載せた時点で，何かしら批判がくるだろうと思い，注視していたら，黒木さんから即日それが飛んできた。この件以外にも， U 検定に関して非常に重要なコメントを発しているので参照しよう。

改めて，経験累積分布関数（ECDF，Empirical Cumulative Distribution Function）のグラフも調べてみよう。 R の基本関数でも作図できるのだが，これまでもしばしば使っている Hmisc パッケージの関数 Ecdf を使ってみる。 R のスクリプトは，先ほどの続きである。

#############
library(Hmisc)

dat<- c(pw, pp)
test<- rep(
   c("Utest", "Perm"), each = k
)

Ecdf(
  dat, group = test,
  label.curves=list(keys= 1:2),
  xlab="p value", lty = 1:2,
  main = "ECDF"
)

###############

結果は，次の図 2 のとおりである。

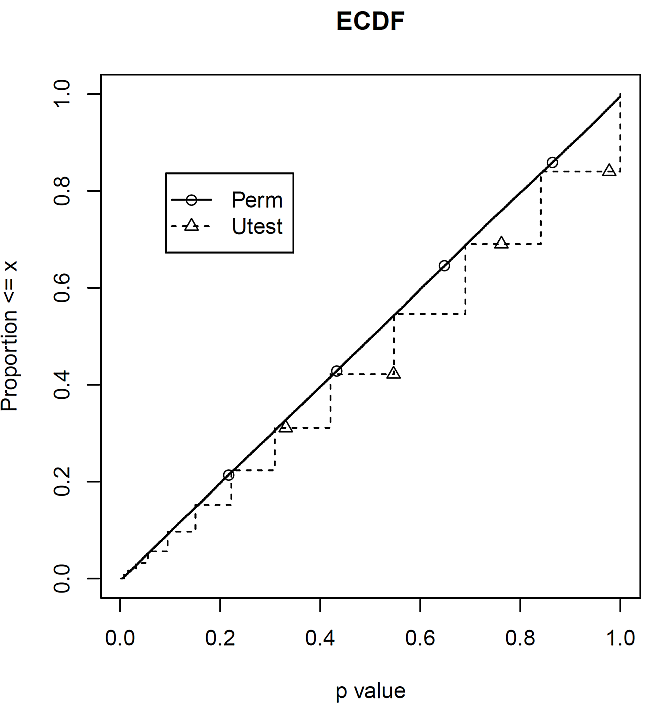
ほぼ対角線上に並ぶ並び替え検定に対して，その対角線から，階段状に着いたり離れたりしながら下振れしている正確 U 検定の違いが分かる。この階段状の変化が，ヒストグラムに反映されるのだが，その反映の仕方が恣意的になってしまう，という欠点を黒木さんは指摘したのである。

さらに，いわゆる 5% 有意水準付近で詳しく見ることにする。

#############
ck<- 1:k/k
df<- c(ck, pw, pp)

test<- relevel(factor(
  rep(c("Theoretical", "U", "Perm"), each = k)
), ref = "Theoretical")

Ecdf(
  df, group = test,
  xlab="p value", label.curves=list(keys= 1:3),
  lty = 1:3,
  main = "ECDF",
  xlim = c(0, 0.1), ylim = c(0, 0.1)
)

abline(v = 0.05, col = "blue")

###############

結果は，次の図 3 のとおりである。

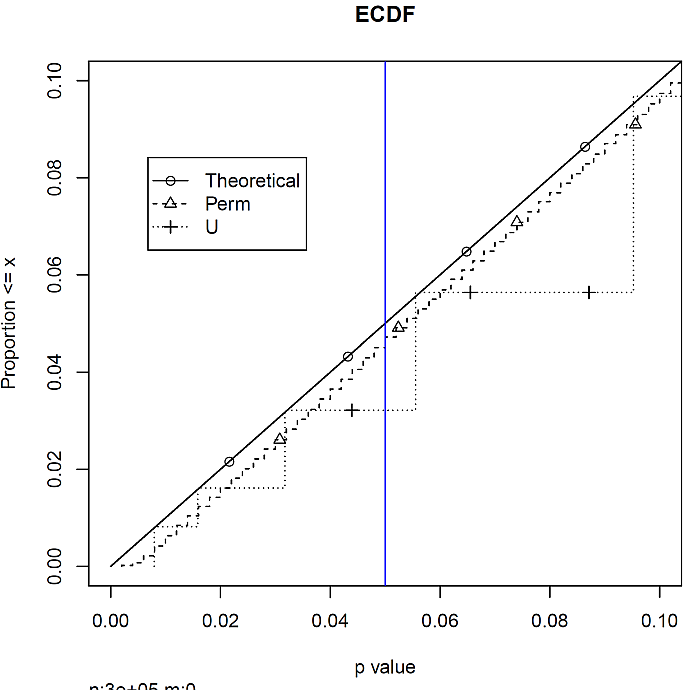
このくらい一部分を拡大すると，並び替え検定にも細かな階段状の変化が見えてくる。しかも，対角線の理論値（理想的な値）より全体的に少し下振れしているのが分かる。正確 U 検定のほうが，階段の先で理論値に近い部分がある。しかし 5% 有意水準点で見ると，正確 U 検定のほうが下振れが大きい。これを 0 から 5% までの合計した棄却率で表わしたのが，次の棒グラフである。

#############
barplot(
 c(
   length(pp[pp < 0.05]), length(pw[pw < 0.05])
   )/k, 
 ylim = c(0, 0.1), col = "#0080ff",
 main = "Nonparametric test for small sample",
 names.arg =c(
      "Permutation",
      "U test"
      ),
 ylab = "Type I error rates with alpha level 0.05"
)
abline(h = 0.05, col = "red", lwd = 2)

###############

結果は，次の図 4 のとおりである。

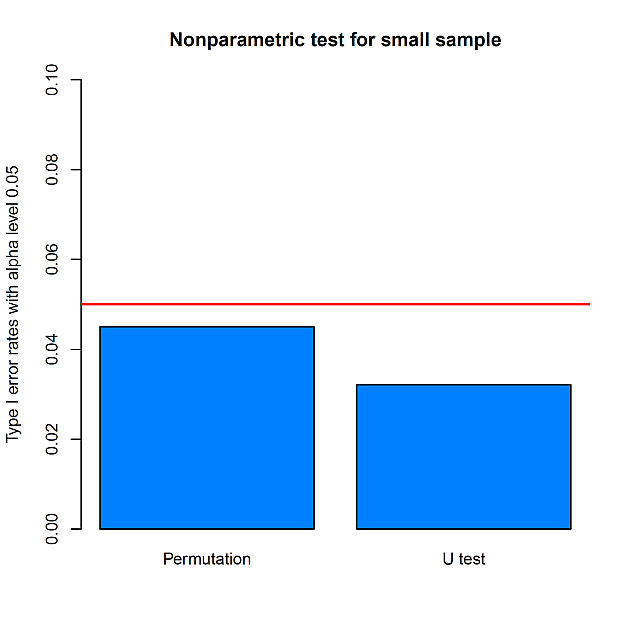
5% と比べて，並び替え検定が少し低く，正確 U 検定がさらに低くなるのは，先ほど 5% 有意水準付近の ECDF の特徴を反映している。

もちろん，この結果は，n = 5 の正規乱数によるシミュレーションである。確率分布や標本サイズが変われば，結果もまた変わりうる。

標本調査の場合，必要な限り大きな標本を確保すべきである，しかしそれが不可能で小標本となってしまった場合，正確 U 検定ではなく，並べ替え検定を利用することも念頭に置いたほうが良い。是非，手元のデータで，結果を比べてみてほしい。

関連サイト

• 多重比較 Steel-Dwass 正規近似と正確検定： U 検定が基準

• 正規性検定をノンパラメトリック検定の選択基準にするな