logo
生物科学研究所 井口研究室
Laboratory of Biology, Okaya, Nagano, Japan
Home

シンプソンのパラドックスと回帰分析・混合モデル：「統計学が最強の学問である」を巡って

井口豊（生物科学研究所，長野県岡谷市）
最終更新：2018年11月9日

1. はじめに

「統計学が最強の学問である」（西内 啓，2013，ダイアモンド社）に，シンプソンのパラドックスの話題が出てくる（p. 180～）。そこでは，以下のようなクロス集計データが出てくる。

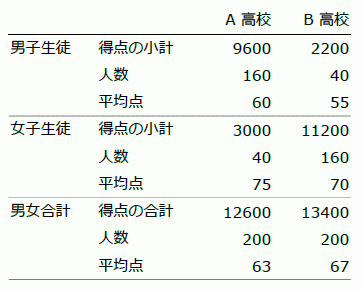
表1. シンプソンのパラドックスの例（西内，2013，p. 181）
シンプソンのパラドックスの例

平均点は，男女ともに，A 高校のほうが 5 点高い。しかしながら，男女合計した全体の平均点は，逆に B 高校のほうが高くなっているのである。このように，集団の部分と全体の統計量に，正反対の結果が生まれる状況をシンプソンのパラドックス（Simpson's paradox）と言う。

西内（2013）は，シンプソンのパラドックスを回避する方法として重回帰分析を挙げているが，この表データ，あるいは，その元になったデータで重回帰分析を行っていない。ここで，このデータを使い，統計ソフト R によって，重回帰分析を含めた，いくつかの分析を行なってみよう。

2. データ解析

A 男，A 女，B 男，B 女の点数データは，まず正規乱数として生成し，それぞれが表 1 に示された平均点になるように調節して利用する。

この場合，2 種類の実験計画（結果として，2 種類の統計モデル）が考えられる。

ひとつは，各生徒を単純に「高校」と「性」分け（生徒に各高校と男女を割り当てた実験，とも言える）クロス構造モデル（crossed model）である。どちらの変数を優先的に扱うか考えない。これは，Excel でも計算できる 2 変数重回帰分析と二元配置分散として扱える。

もうひとつのモデルは，生徒をまず「高校」で分け，各高校の中で「男女」に分けた階層モデルである，ネスト構造モデル（nested model）である。これをネスト分散分析（nested anova）と線形混合モデル（linear mixed model）でやってみよう。

なお，どちらの高校の男女平均差も等しいので，交互作用を考える必要なく，それゆえ交互作用無しのモデルとする。

まず，クロス構造モデルとして分析してみる。 

# クロス構造モデル

# A 高校，B 高校
school<- factor(rep(c("A", "B"), c(200, 200)))

# 男 m，女 f
sex<- factor(rep(
c("m", "f", "m", "f"), c(160, 40, 40, 160)
))

# テスト点数
set.seed(100)

set.seed(100)
y1<- rnorm(160)
y2<- rnorm(40)
y3<- rnorm(40)
y4<- rnorm(160)

score1<- 60 - mean(y1) + y1
score2<- 75 - mean(y2) + y2
score3<- 55 - mean(y3) + y3
score4<- 70 - mean(y4) + y4

score<- c(score1, score2, score3, score4)

# 線形重回帰分析
mod.1<- lm(score ~ school + sex)
summary(mod.1)

# 二元配置分散分析
summary(aov(score ~ school + sex))

重回帰分析の結果は次のようになる。 

              Estimate Std. Error    t value Pr(>|t|)    
(Intercept)  7.500e+01  9.196e-15  8.156e+15   <2e-16 ***
schoolB     -5.000e+00  9.386e-15 -5.327e+14   <2e-16 ***
sexm        -1.500e+01  9.386e-15 -1.598e+15   <2e-16 ***

二元配置分散分析の結果は次のようになる。 

             Df Sum Sq Mean Sq   F value Pr(>F)    
school        1   1600    1600 2.838e+29 <2e-16 ***
sex           1  14400   14400 2.554e+30 <2e-16 ***
Residuals   397      0       0

自由度 n の t 値と自由度 (1, n) の F 値は同値なので，二元配置分散分析は重回帰分析そのものであると言える。ただし，二元配置分散分析として出力すると，点数がどのように扱われたか，それが分からない点が欠点である。重回帰分析ならば，B 高校が 5 点低いと出力され，西内（2013）言う「直感的どおりの結果」（p. 185）となることが分かる。

ただし，重回帰分析でも，両校の何点を比較して5点差と考えるのか，理解しにくい欠点がある。単純に結果を考えると，切片 75 は A 高校女子の平均なので，これと比べて B 高校は 5 点低い，という判断になる。しかし，どうも，しっくりしない。

次に，ネスト構造モデルとして分析してみる。データは，上記のクロス構造モデルと同じなので，スクリプトは，分析部分だけを示す。 

# ネスト構造モデル

# ネスト分散分析
summary(aov(score ~ school + Error(sex)))

library(lmerTest)
# 線形混合モデル，ランダム切片
mod2<- lmer(score ~ school + (1|sex))
summary(mod2)

# 線形混合モデルの結果で平均の比較
lsmeansLT(mod2)

まず，ネスト分散分析の結果を示す。 

Error: Within
           Df Sum Sq Mean Sq F value Pr(>F)    
school      1 1600.0    1600    1638 <2e-16 ***
Residuals 397  387.8       1

クロス構造モデルの結果で述べたように，検定は可能だが，各高校の平均点数の情報が不明である。

線形混合モデルの結果は次のようになる。 

Fixed effects:
            Estimate Std. Error       df t value Pr(>|t|)    
(Intercept)  67.4997     7.5002   0.6000    9.00     0.15    
schoolB      -4.9994     0.1235 396.5000  -40.47   <2e-16 ***

切片が約 67.5 であり，高校 B がそれより約 5 点低いことが分かる。 t 値の二乗を計算すると，ネスト分散分析の F 値に，ほぼ等しいことが分かる。各高校の平均点の情報は lsmeansLT 関数によって明瞭になる。 

Least Squares Means table:
          school Estimate Standard Error  DF t-value Lower CI Upper CI
school  A    1.0    67.50           7.50 1.7    9.00     30.2    104.8
school  B    2.0    62.50           7.50 1.7    8.33     25.2     99.8

つまり，混合モデルでは，両校の平均を次のように考えているのである。

これは，それぞれの高校の男女の平均を平均した値に相当する。

この比較のほうが，重回帰分析における A 高校女子の平均を基準にした比較よりも，「直感的に」すっきりした感じがする。

話題が変わるが，本書の中に，サンプル数という言葉が何度か出てくる（例えば，p.52）。しかし，それは，正しくは，サンプルサイズである（参照：サンプル数とサンプルサイズ n は意味が違う）

初学者向けとも言える書籍で，このような用語の間違いを見ると，実にガッカリする。「統計学者ならば、サンプル数という言葉は使いません」という説明をしているウェブサイトもある（参照：サンプル数とは何か？）。その意味で，西内（2013）も正確に書いてほしかった。

Home