中央値と平均の効果量: Mangiafico's d and Cohen's d
井口豊(生物科学研究所,長野県岡谷市)
最終更新: 2024 年 1 月 22 日
1. はじめに
平均の差の効果量(effect size)として有名なものが Cohen の d であるが,それに相当するような中央値の差の効果量として, Mangiafico の d がある。
統計ソフト R では, rcompanion パッケージの mangiaficoD 関数を使うと,その効果量が計算される。
それは,二つの標本の中央値を med1, med2, 中央絶対偏差 (median absolute deviation) を MAD1, MAD2 とすると,以下のような式で表される。
\begin{eqnarray} \text{Mangiafico's}\ d=\frac{med_{1}-med_{2}}{\sqrt{\frac{{MAD_1}^2 + {MAD_2}^2}{2}}} \end{eqnarray}ただし, R で使われる中央絶対偏差の関数 mad は,デフォルトで係数 1.4826 が付いている(mad マニュアル)。これは,標本が正規分布に従い,かつ,そのサイズが大きくなると,漸近的に中央絶対偏差が標準偏差になるように調整されているのである。
したがって,このような条件のもとでは, Mangiafico d と Cohen の d は同等なものになる。
以下に, R によるシミュレーションで確かめてみよう。二つの標本サイズを 10000 として,標準正規分布の平均(中央値でもある)の差を 0 から 3 までランダムに変えて,これら二つの効果量を計算する。
#############
library(effectsize)
library(rcompanion)
n<- 10000
set.seed(1)
d<- replicate(100, {
x1<- rnorm(n)
x2<- x1 + runif(1, 0, 3)
c(
mangiaficoD(x = x2, y = x1),
cd<- cohens_d(x = x2, y = x1)$Cohens_d
)
})
summary(d[1, ])
summary(d[2, ])
plot(
d[1, ], d[2, ],
xlim = c(0, 3),
ylim = c(0, 3),
col = "blue",
xlab = "Mangiafico's d",
ylab = "Cohen's d"
)
abline(
0, 1,
col = "red",
lwd = 1.6
)
################
結果は,次の図 1 のとおりである。
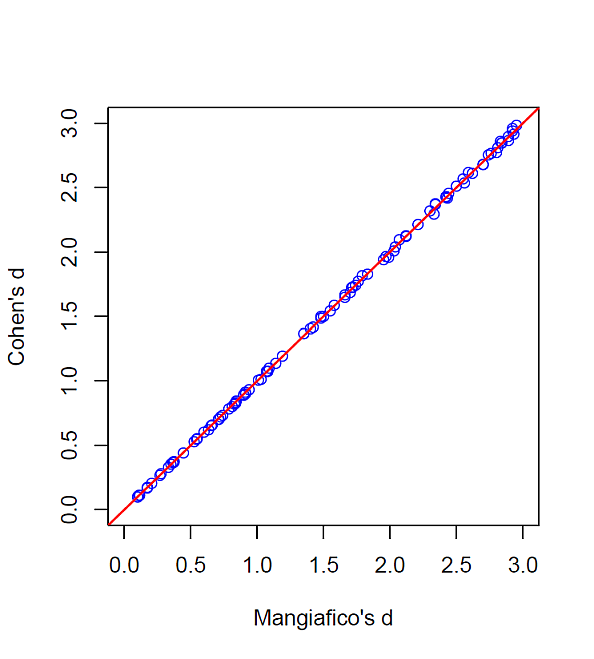
両者がよく一致することがわかり, Mangiafico の d が中央値の差に対して, Cohen の d と同様な意味を持つ効果量だと言える。
なお,マン-ホイットニー U 検定 (Mann-Whitney U test) は,中央値検定ではなく,順位平均検定なので, Mangiafico の d を適用すべきではない。
U 検定の効果量は,いくつか種類があり,前述の mangiaficoD 関数の製作者でもある Mangiafico の以下の解説ページ参照してほしい。
このページには, Vargha and Delaney's A, Cliff's delta, Glass rank biserial coefficient, r, Kendall’s tau-b, Freeman's theta, epsilon-squared などが書かれている。これらの中で,日本人に馴染み深いのは, z 値から計算される r だろう。