logo
生物科学研究所 井口研究室
Laboratory of Biology, Okaya, Nagano, Japan
Home

二重積分を R と Maxima で解く

井口豊（生物科学研究所，長野県岡谷市）
最終更新：2024 年 4 月 22 日

二重積分の積分区間が定数でなく，変数の場合，数値解析ソフト Maxima と統計解析ソフト R で数値解を求めるには，どうすれば良いか？例えば，次の式を考えてみる。

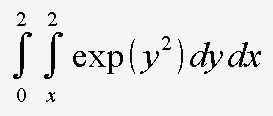
指数関数の二重積分

二重積分と言っても驚くことはなく，この場合，通常の単積分を 2 回繰り返せば良い。

まず， Maxima のプログラム。 

f(y):= exp(y^2);
g(x):=integrate(f(y), y, x, 2);
integrate(g(x), x, 0, 2);
float(%);

結果は，以下のとおり。

\begin{eqnarray} \frac{e^4-1}{2} \end{eqnarray}

26.79907501657212

解析的に解いた結果と数値積分の結果を返してくれる。

次に， R による数値解の求め方。 

g<- function(x){
  f<- function(y){
  exp(y^2)
  }
  integrate(f, x, 2)$value
}
integrate(Vectorize(g), 0, 2)

注意する点は，二回目の積分，つまり，関数 g の積分で， Vectorize 関数を使い，関数をベクトル化することである。

結果
26.79908 with absolute error < 1.3e-12

詳細には検討していないが，実質的に Maxima と同じになる。

Home