logo
生物科学研究所 井口研究室
Laboratory of Biology, Okaya, Nagano, Japan
Home

Cox 比例ハザードと制限付き 3 次スプラインモデル

井口豊（生物科学研究所，長野県岡谷市）
最終更新： 2023 年 3 月 11 日

1. はじめに

　生存時間解析の代表的なモデルとして，Cox 比例ハザード（cox proportional hazard, CPH）が良く知られている。簡単に， Cox 回帰とも呼ばれる。ただし，これは文字通り，比例ハザードが成り立つことを前提としたモデルなのだが，実際には，そのようにならないこともある。ここでは，そのような例を取り上げて，制限付き 3 次スプライン（restricted cubic spline, RCS）回帰モデルを適用してみる。

2. Cox 回帰と制限付き 3 次スプライン回帰に対する比例ハザード性の検定

議論を単純にするために，単変量 Cox 回帰を考える。データには，統計ソフト R のパッケージ survival の原発性胆汁性胆管炎データ pbc (Mayo Clinic Primary Biliary Cholangitis Data) を利用し，年齢 age を説明変数として利用した。 status は便宜上， 0 (censored) とそれ以外に分けた。

作図には，パッケージ survminer を利用し，比例ハザード性の検定には， Schoenfeld 残差検定を使った。なお，この検定結果をグラフ化する ggcoxzph 関数の信頼区間（2 SE で近似）にはバグがあり， GitHub から修正プログラムが出ている。以下のサイト参照。

具体的なスクリプトは以下のようになる。 


#############
# パッケージとデータ
library(survival)
library(survminer) # 修正プログラム
library(rms)
library(cowplot)

dat<- na.omit(pbc)
head(dat)

# Cox 回帰
cox.mod<- cph(
     Surv(time, status > 0) ~ age, data =  dat
)
anova(cox.mod)

# 比例ハザード性の Schoenfeld 残差検定
cox.ph <- cox.zph(cox.mod)
cox.ph

pcox.ph<- round(cox.ph$table[1,3], 2)

# RCS 回帰
k <- with(dat, quantile(age, c(0.25, 0.5, 0.75)))

rcs.mod<- cph(
    Surv(time,status > 0) ~ rcs(age, k),
    data = dat
)
anova(rcs.mod)

# 比例ハザード性の Schoenfeld 残差検定
rcs.ph <- cox.zph(rcs.mod)
rcs.ph

prcs.ph<- round(rcs.ph$table[1,3], 2)

# Schoenfeld 検定グラフ
g.coxph_test<- ggcoxzph(cox.ph[1], main = "")
g.rcsph_test<- ggcoxzph(rcs.ph[1], main = "")

plot_grid(
   print(g.coxph_test), print(g.rcsph_test),
   labels = c(
       paste("Cox, Schoenfeld test p = ", pcox.ph),
       paste("RCS, Schoenfeld test p = ", prcs.ph)
     )
)

# 年齢の相対ハザード比グラフ
ddist <- datadist(dat)
options(datadist = "ddist")

g.cox<- plot(
        Predict(cox.mod, age), ylim = c(-1, 1.5)
)
g.rcs<- plot(
        Predict(rcs.mod, age), ylim = c(-1, 1.5)
)

plot_grid(
   g.cox, g.rcs,
   labels = c("Cox model", "RCS model")
)

################

結果は以下の通りである。 まず，年齢に対する Schoenfeld の比例ハザード性検定の結果を示す。

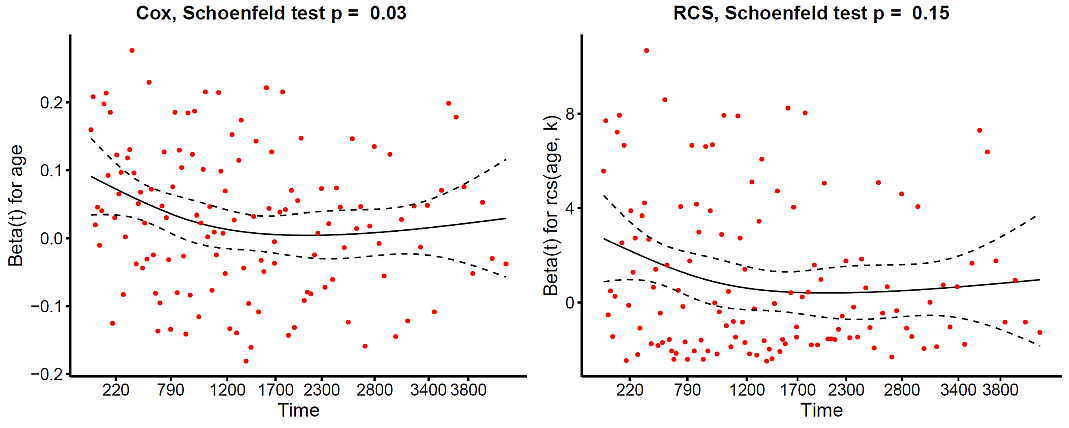
年齢の比例ハザード性

図 1. 年齢に対する比例ハザード性検定

単純な Cox 回帰（グラフ左）では，その前提である比例ハザード性が満たされないが， RCS 回帰（グラフ右）では，それが満たされることが分かる。両者のグラフを比べると，上部（高年齢のデータ）では，ほぼ同様な分布になっているが，下部（低年齢のデータ）では， RCS 回帰のほうが密集した分布になっていることが分かる。

次に，年齢と相対ハザードの関係のグラフである。

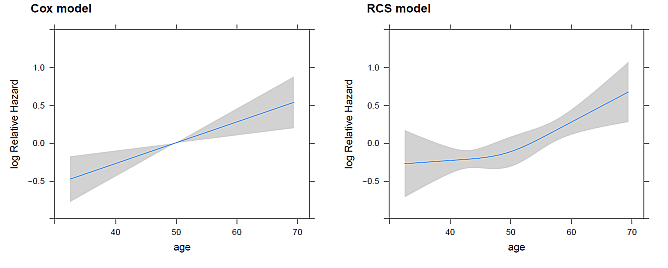
年齢と相対ハザードの関係

図 2. 年齢と相対ハザードの関係

単純な Cox 回帰（グラフ左）と比べて， RCS 回帰（グラフ右）では，低年齢では相対ハザードの変化が緩やかであることが分かる。

関連ページ

Home