回帰分析: x, y 誤差がある場合 SMA, MA 回帰

井口豊（生物科学研究所，長野県岡谷市）
最終更新： 2023 年 12 月 23 日

1. はじめに

一般的に学校で教えられる回帰分析や回帰式は，通常最小二乗法（Ordinary Least Square: OLS）回帰である。 Excel で計算され，グラフ化される回帰式もそうである。わざわざ「通常」と呼ばれるからには，そうではない回帰式もある。そのことは，別サイトに既に書いた。

回帰と相関，知っているようで知らない，その本質：Excel の回帰分析を例として

OLS 回帰では， y の誤差変動に注目し， y 軸方向の距離のみを最小とするように計算される（上記サイト図 2）。

一方で， x, y の両方の誤差を考慮した回帰分析の代表的なものが MA (Major axis) や SMA (Standardised major axis) である。前者は，主成分回帰，主軸回帰，最大軸回帰などとも呼ばれる。文字通り，主成分分析と同様な計算を行う。後者は，標準化主軸回帰と呼ばれるが，標準主軸 (Standard major axis) 回帰，縮小長軸 (Reduced major axis, RMA) 回帰，幾何平均 (Geometric mean) 回帰と呼ばれることもある。このように，日本語でも，英語でも，同じものに対して名称が乱立するのは，統計学では頻繁にある。

私の研究では， MA 回帰に関しては，ゲンジボタルとヘイケボタルにおいて，雌雄の平均体長の関連を調べるのに利用した（井口，2007）。

一方， SMA 回帰に関しては，ヒメボタルのアロメトリーを調べるのに利用した（Iguchi, 2023）。私の研究ではないが，日本の樹木研究としては珍しく，剪定条件による樹木成長の違いを調べるのにアロメトリーが利用された最近の研究がある（Shimada, 2023）。

文献情報は，最後の参考文献に一括した。

OLS, SMA, MA の回帰分析の使い分けに関しては，以下の解説が参考になる。

本サイトでは， SMA 回帰に焦点を当てて， OLS 回帰と比較して論じる。統計ソフト R パッケージでは， lmodel2 や smatr で計算することができる。グラフを描くならば lmodel2，回帰分析に関連した色々な計算をするなら smatr が便利だ。 smatr は， R パッケージになる以前から，古生物学 Paleobiology 分野では良く知られた回帰分析ソフトであった。例えば， Australopithecus anamensis の犬歯の形状分析に smatr を利用した Manthi et al. (2012) の研究がある

2. OLS 回帰と SMA 回帰の比較

以下のような 2 次元の仮想データセット
(s, t)
を考え，まず， OLS 回帰で分析する。


#############
s<- rep(seq(10, 100, by = 10), each = 3)
t<- rep(seq(-10, 10, by = 10), 10)

mod<- lm(t ~ s)

round(
  summary(mod)$coef, 3
)

plot(
  s, t,
  xlim = c(0, 100),
  ylim = c(-100, 100),
  col = "blue"
)
abline(mod, col = "red")

################

結果は以下の通りである。 summary の一部とグラフを示す。


################################################
            Estimate Std. Error t value Pr(>|t|)
(Intercept)        0      3.333       0        1
s                  0      0.054       0        1

################################################

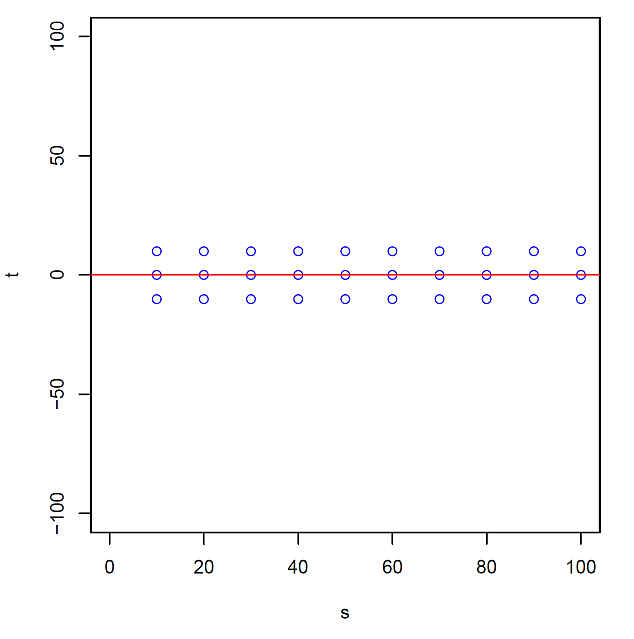
変数 s に対する t の OLS 回帰

図 1.変数 s に対する t の OLS 回帰直線

t = 0 となる定数項だけの回帰式で近似されるデータ分布であることが分かる。

次に，データ点 (s, t) を原点 (0, 0) を中心として時計回りに 45° 回転させて (x, y) に移動させたデータ集合を考えてみる。大学 1, 2 年の線形代数で学ぶ行列による 1 次変換で計算できる。

\[ \begin{pmatrix} x \\ y \end{pmatrix}= \begin{pmatrix} \cos\frac{\pi}{4} & -\sin\frac{\pi}{4} \\ \sin\frac{\pi}{4} & \cos\frac{\pi}{4} \end{pmatrix} \begin{pmatrix} s \\ t \end{pmatrix} \]

この計算自体は簡単なので， R にデータを読み込ませるときは，次のように， x, y をそれぞれ s, t で表わしても良い。

\[ x=\frac{s}{\sqrt{2}}-\frac{t}{\sqrt{2}} \] \[ y=\frac{s}{\sqrt{2}}+\frac{t}{\sqrt{2}} \]

以下のスクリプトでは，回転変換から R のコードを利用して計算している。その上で，原点を中心に時計回りに 45° 回転させて (x, y) に移動させたデータに， OLS 回帰と SMA 回帰をフィットさせている。 s, t データは前述のものを受け継いでいる。


#############
# (s, t) を原点中心に 45度回転
theta<- pi/4

rot<- function(s, t) {
   matrix(c(
      cos(theta), -sin(theta),
      sin(theta), cos(theta)
     ), byrow = TRUE, ncol = 2) %*%
   matrix(c(
      s,
      t
    ))
}

# 変換後の (s, t) を (x, y) とする。 
x<- mapply(rot, s, t)[1, ]
y<- mapply(rot, s, t)[2, ]


# パッケージ lmodel2 利用の回帰分析
library(lmodel2)

mod<- lmodel2(
     y ~ x,
    range.y = NULL,
    range.x = NULL,
    nperm = 1000
)

# 詳細な結果
mod

# 定数項と傾き
data.frame(
    lapply(mod$regression.results, 
       function (x) if(is.numeric(x)) round(x, 3) else x
      )
)

# グラフ
# OLS
plot(
  mod, "OLS",
  xlim = c(0, 100),
  ylim = c(0, 100),
  col = "blue"
)

# SMA
plot(
  mod, "SMA",
  xlim = c(0, 100),
  ylim = c(0, 100),
  col = "blue"
)

# パッケージ smatr 利用の回帰分析
library(smatr)

mod.ols<- sma(
   y ~ x,
   method = "OLS",
   slope.test = 1,
   elev.test = 0
)

mod.sma<- sma(
   y ~ x,
   method = "SMA",
   slope.test = 1,
   elev.test = 0
)

# 詳細な結果
# OLS
mod.ols

# SMA
mod.sma

# OLS 定数項と傾き
round(as.data.frame(mod.ols$coef), 3)

# SMA 定数項と傾き
round(as.data.frame(mod.sma$coef), 3)

################

結果は以下の通りである。詳細な出力は省略して，定数項，傾きとグラフを示す。


################################################
# パッケージ lmodel2 利用の定数項と傾き
  Method Intercept Slope Angle..degrees. P.perm..1.tailed.
1    OLS     5.815  0.85           40.38             0.001
2     MA     0.000  1.00           45.00             0.333
3    SMA     0.000  1.00           45.00                NA

# パッケージ smatr 利用の定数項と傾き
# OLS
          coef.reg. lower.limit upper.limit
elevation     5.815      -3.196      14.827
slope         0.850       0.647       1.054

# SMA
          coef.SMA. lower.limit upper.limit
elevation         0      -9.094       9.094
slope             1       0.817       1.224

################################################

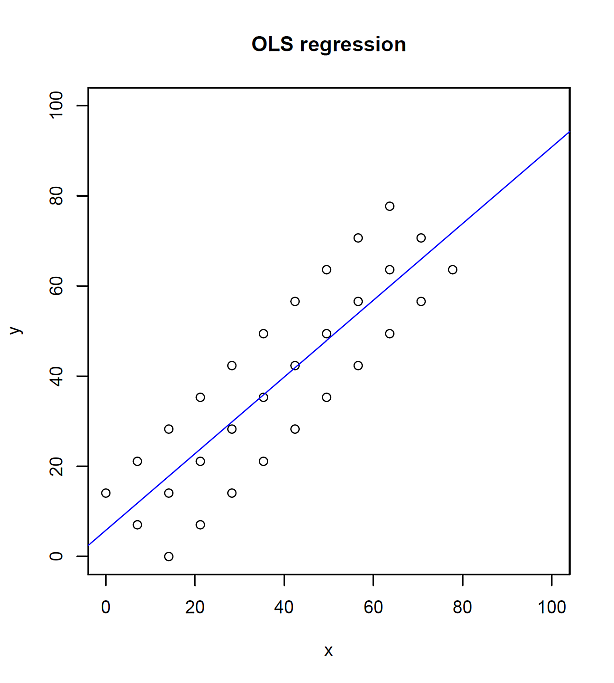
変数 x に対する y の OLS 回帰

図 2.変数 x に対する y の OLS 回帰直線

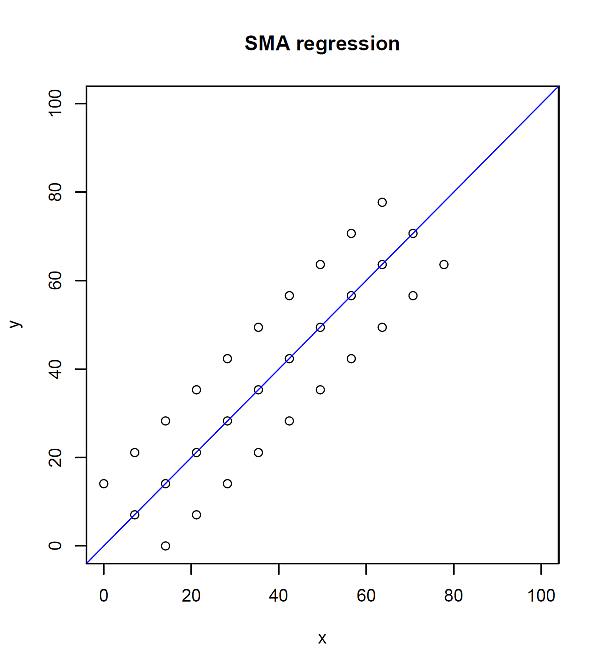
変数 x に対する y の SMA 回帰

図 3.変数 x に対する y の SMA 回帰直線

SMA 回帰直線は（そして MA 回帰直線も），x, y 両方の誤差を考慮して計算するので，傾き 1 （45°），切片 0 となるが， OLS 回帰直線は y の誤差しか考慮していないため，そうならないことが分かる。

参考文献

井口豊（2007）ゲンジボタルとヘイケボタルにレンシュの法則はあてはまるか？. 全国ホタル研究会誌 40: 32-34.

Iguchi Y. (2023) Allometric approach to the two male morphs in the Japanese firefly Luciola parvula. Frontiers in Insect Science, 3, 1230363.

Manthi F. K., Plavcan J. M. and Ward C. V. (2012) New hominin fossils from Kanapoi, Kenya, and the mosaic evolution of canine teeth in early hominins. South African Journal of Science 108(3): 1-9.

Shimada H. (2023) Effects of Pruning Types on Tree Vigor of Bamboo-Leaf Oak Inferred from Allometric Analysis. American Journal of Plant Sciences, 14, 1430-1438. DOI: 10.4236/ajps.2023.1412096

Home